
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点.
(1)求证:△ABC为等边三角形.
(2)求DE的长.
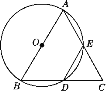
【答案】(1)详见解析;(2)DE=1.
【解析】
(1)连接AD,利用直径所对的圆周角为直角及垂直平分线的性质得到相等的线段AB=AC,联立已知的AB=BC,即可证得△ABC是等边三角形;
(2)连接BE,利用直径所对的圆周角为直角,得到BE⊥AC,然后利用等腰三角形三线合一的性质得出E为AC的中点,继而利用三角形中位线的数量关系求得DE的长度.
(1)连接AD.
∵AB是⊙O的直径,∴∠ADB=90°.
∵点D是BC的中点,∴AD是线段BC的垂直平分线,∴AB=AC.
∵AB=BC,∴AB=BC=AC,∴△ABC为等边三角形.
(2)连接BE.
∵AB是直径,∴∠AEB=90°,∴BE⊥AC.
∵△ABC是等边三角形,∴AE=EC,即E为AC的中点.
∵D是BC的中点,∴DE为△ABC的中位线,∴DE=![]() AB=
AB=![]() ×2=1.
×2=1.


科目:初中数学 来源: 题型:
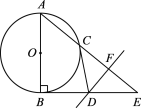
【题目】如图,在Rt△ABE中,∠B=90°,以AB为直径的⊙O交AE于点C,CE的垂直平分线FD交BE于D,连接CD.
(1)判断CD与⊙O的位置关系,并证明;
(2)若AC·AE=12,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
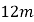
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
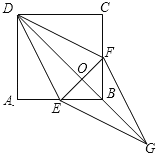
【题目】如图,在正方形ABCD中,点E、F分别在边AB、BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连结DB交EF于点O,延长OB至点G,使OG=OD,连结EG、FG,判断四边形DEGF是否是菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工厂要选一块矩形铁皮加工成一个底面半径为20 cm,高为![]() cm的圆锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少厘米的矩形铁皮,才能使所用材料最省?
cm的圆锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少厘米的矩形铁皮,才能使所用材料最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,连结BD.
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由.
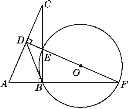
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程4kx2-4kx+k+1=0的两个实数根,是否存在实数k,使(2x1-x2)(x1-2x2)=-![]() 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com