练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】疫情防控，我们一直在坚守．某居委会组织两个检查组，分别对“居民体温”和“居民安全出行”的情况进行抽查．若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查，则他们恰好抽到同一个小区的概率是（ ）

    A.B.C.D.

    【答案】A

    【解析】

    将三个小区分别记为A、B、C，列举出所有等情况数和他们恰好抽到同一个小区的情况数，然后根据概率公式即可得出答案．

    将三个小区分别记为A、B、C，根据题意列表如下：

    A

    B

    C

    A

    （A，A）

    （B，A）

    （C，A）

    B

    （A，B）

    （B，B）

    （C，B）

    C

    （A，C）

    （B，C）

    （C，C）

    由表可知，共有9种等可能结果，其中他们恰好抽到同一个小区的有3种情况，
    所以他们恰好抽到同一个小区的概率为.
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

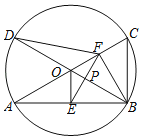
    【题目】如图，已知AC，BD为⊙O的两条直径，连接AB，BC，OE⊥AB于点E，点F是半径OC的中点，连接EF．

    （1）设⊙O的半径为1，若∠BAC＝30°，求线段EF的长．

    （2）连接BF，DF，设OB与EF交于点P，

    ①求证：PE＝PF．

    ②若DF＝EF，求∠BAC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某游泳馆推出了两种收费方式．

    方式一：顾客先购买会员卡，每张会员卡200元，仅限本人一年内使用，凭卡游泳，每次游泳再付费30元．

    方式二：顾客不购买会员卡，每次游泳付费40元．

    设小亮在一年内来此游泳馆游泳的次数为次（为正整数）．

    （1）根据题意，填写下表：

    游泳次数

    5

    10

    15

    …

    方式一的总费用（元）

    350

    650

    …

    方式二的总费用（元）

    200

    400

    …

    （2）若小亮计划今年游泳的总费用为2000元，选择哪种付费方式，他游泳的次数比较多；

    （3）当时，小亮选择哪种付费方式更合算．并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

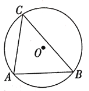
    【题目】问题提出

    （1）如图，是的弦，点是上的一点，在直线上方找一点，使得，画出，并说明理由；

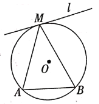
    问题探究

    （2）如图，是的弦，直线与相切于点，点，是直线上异于点的任意一点，请在图中画出图形，试判断的大小关系；并说明理由；

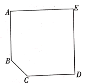
    问题解决

    （3）如图，有一个平面图为五边形ABCDE的展览馆，其中，，．展览馆保卫人员想在线段上选一点安装监控装置，用来监视边，现只要使最大，就可以让监控装置的效果达到最佳，问在线段上是否存在点，使最大？若存在，请求出符合条件的的长，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，点D是AB下方圆上的一点，点C是优弧AD的中点，过点B作⊙O的切线BE交AC的延长线于点E，连接OC，OD，CB，BD．

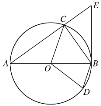
    （1）求证：BD∥OC；

    （2）当AB＝6时，完成填空：

    ①当BE＝ 时，四边形ODBC是菱形；

    ②当BE＝ 时，S△BCE＝S△ABC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题背景：如图 1，在和中，，连接 交的延长线于点．则的值是____________．

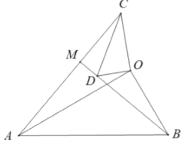
    问题解决：如图 2，在问题背景的条件下，将绕点在平面内旋转，点始终在的外部，所在直线交于点，若，当点与点重合时，的长是____________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线经过点，交轴于点.

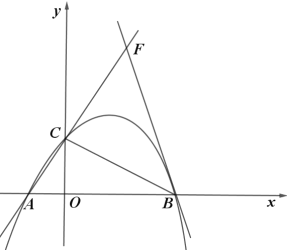
    （1）求抛物线的函数表达式；

    （2）点为轴右侧抛物线上一点，是否存在点使？若存在，求出点的坐标，若不存在，请说明理由.

    （3）将直线绕点顺时针旋转，与直线相交于点，求直线的函数表达式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，且AB＝4，点C是弧AB上的一动点（不与A，B重合），过点B作⊙O的切线交AC的延长线于点D，点E是BD的中点，连接EC．

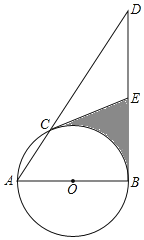
    （1）若BD＝8，求线段AC的长度；

    （2）求证：EC是⊙O的切线；

    （3）当∠D＝30°时，求图中阴影部分面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

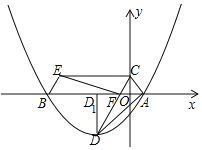
    【题目】如图,在平面直角坐标系中，抛物线与x轴交于点A(1, 0),B(-7, 0),顶点D坐标为(-3,)，点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.过顶点D作DD1⊥x轴于点D1

    (1)求抛物线的表达式

    (2)求证:四边形BFCE是平行四边形．

    (3)点P是抛物线上一动点，当P在B点左侧时,过点P作PM⊥x轴,点M为垂足,请问是否存在P点使得△PAM与△DD1A相似,如果存在，请写出点P的横坐标．

    查看答案和解析>>

    同步练习册答案