
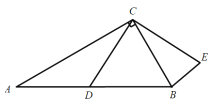
【题目】问题提出
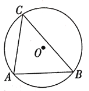
(1)如图,![]() 是
是![]() 的弦,点
的弦,点![]() 是
是![]() 上的一点,在直线
上的一点,在直线![]() 上方找一点
上方找一点![]() ,使得
,使得![]() ,画出
,画出![]() ,并说明理由;
,并说明理由;
问题探究
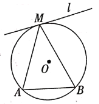
(2)如图,![]() 是
是![]() 的弦,直线
的弦,直线![]() 与
与![]() 相切于点
相切于点![]() ,点
,点![]() ,是直线
,是直线![]() 上异于点
上异于点![]() 的任意一点,请在图中画出图形,试判断
的任意一点,请在图中画出图形,试判断![]() 的大小关系;并说明理由;
的大小关系;并说明理由;
问题解决
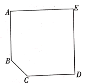
(3)如图,有一个平面图为五边形ABCDE的展览馆,其中![]() ,
,![]() ,
,![]() .展览馆保卫人员想在线段
.展览馆保卫人员想在线段![]() 上选一点
上选一点![]() 安装监控装置,用来监视边
安装监控装置,用来监视边![]() ,现只要使
,现只要使![]() 最大,就可以让监控装置的效果达到最佳,问在线段
最大,就可以让监控装置的效果达到最佳,问在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 最大?若存在,请求出符合条件的
最大?若存在,请求出符合条件的![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
【答案】(1)见解析 (2)∠AMB>∠AM1B,理由见解析; (3)存在;![]()
【解析】
(1)根据同弧所对的圆周角相等即可作图求解;
(2)根据三角形的外角定理即可作图求解;
(3)作经过点![]() 、
、![]() 且和
且和![]() 相切的
相切的![]() ,切点为
,切点为![]() ,由(2)可知此时
,由(2)可知此时![]() 最大,连接
最大,连接![]() 、
、![]() ,分别延长
,分别延长![]() 、
、![]() 交于点
交于点![]() ,证明四边形
,证明四边形![]() 是正方形,再求出
是正方形,再求出![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,由正方形的性质可得,
,由正方形的性质可得,![]() ,
,![]() ,再证明
,再证明![]() 垂直平分线段
垂直平分线段![]() ,再根据圆的性质可得
,再根据圆的性质可得![]() ,连接
,连接![]() ,可得
,可得![]() ,则
,则![]() ,设
,设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,![]() ,在
,在![]() 中,利用勾股定理得到
中,利用勾股定理得到![]() 又利用
又利用![]() 得到OG=
得到OG= ![]() ,故可得到方程,求出R,再求出此时DM的长即可.
,故可得到方程,求出R,再求出此时DM的长即可.
解:(1)如图:
在优弧![]() 上任意取一点
上任意取一点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() .
.
理由:![]() ,
,
∴![]() .
.
(2)![]() 如图,
如图,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵![]() 是
是![]() 的外角,
的外角,
∴![]() ,
,
∵![]()
∴![]()
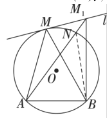
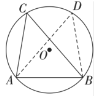
(3)作经过点![]() 、
、![]() 且和
且和![]() 相切的
相切的![]() ,切点为
,切点为![]() ,由(2)可知此时
,由(2)可知此时![]() 最大,
最大,
连接![]() 、
、![]() ,分别延长
,分别延长![]() 、
、![]() 交于点
交于点![]()
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∵![]()
∴四边形![]() 是正方形。
是正方形。
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
连接![]() ,交
,交![]() 于点
于点![]() ,由正方形的性质可得,
,由正方形的性质可得,![]() ,
,
![]() ,
,
∵BF=CF,OB=OC
∴![]() 垂直平分线段
垂直平分线段![]() ,
,
∴圆心![]() 在线段
在线段![]() 上,
上,![]()
连接![]() ,则
,则![]() ,则
,则![]() ,
,
设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]()
∵![]()
∴![]() ,
,
∴![]() ,
,
解得![]() (不合题意,舍去)或
(不合题意,舍去)或![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在线段![]() 上存在点
上存在点![]() ,使
,使![]() 最大,符合条件的
最大,符合条件的![]() 的长为
的长为![]() .
.


科目:初中数学 来源: 题型:
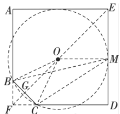
【题目】某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
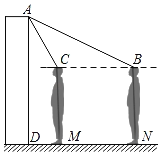
【题目】在新冠病毒疫情防控期间,某校“停课不停学”,开展了网络教学.为了解九年级学生在网络学习期间英语学科和数学学科的学习情况,复课后从九年级学生中随机抽取60名学生进行了测试,获得了他们成绩(百分制)的数据,通过对成绩数据的整理、描述和分析,得到了如下部分信息.
①英语成绩的频数分布直方图如图:
(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100.)
②英语和数学成绩的平均数、中位数、众数如表:
学科 | 平均数 | 中位数 | 众数 |
英语 | 74.8 | m | 83 |
数学 | 72.2 | 70 | 81 |
③英语成绩在70≤x<80这一组的数据是:
70 71 72 73 73 73 74 76 77 77 77 78 79 79
根据以上信息,回答下列问题:
(1)表中m的值是 .
(2)在此次测试中,李丽的英语成绩为74分,数学成绩为71分,该名学生成绩排名更靠前的学科是 .(填“英语”或“数学”),理由是 .
(3)若该校九年级共有500名学生,请你估计英语成绩超过77.5分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=30°,∠ACB=90°,BC=2,D是AB上的动点,将线段CD绕点C逆时针旋转90°,得到线段CE,连接BE,则BE的最小值是( )
A.![]() -1B.
-1B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“停课不停学,学习不延期!”某市教育局为了解初中学生疫情期间在家学习时对一些学习方式的喜好情况,通过微信采用电子问卷的方式随机调查了部分学生(电子调查表如图所示),并根据调查结果绘制了如下尚不完整的统计图,
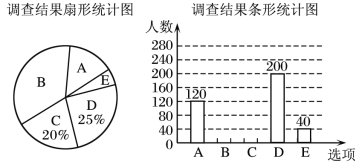
根据以上统计图,解答下列问题:
(1)本次接受调查的学生共有 人;
(2)补全条形统计图;
(3)扇形统计图中,扇形B的圆心角的度数是 度;
(4)若该市约有16万初中生,请估计喜欢自学(选择选项C和D)的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情防控,我们一直在坚守.某居委会组织两个检查组,分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查,则他们恰好抽到同一个小区的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
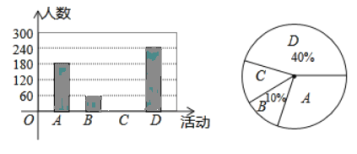
【题目】为了丰富居民的文化生活.某社区开展跳舞、绘画、游泳、唱歌等活动来让居民娱乐.为了解居民对跳舞、绘画、游泳、唱歌这四种活动(以下分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示这四种不同活动)的喜爱情况,在“五一”劳动节期间对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
表示这四种不同活动)的喜爱情况,在“五一”劳动节期间对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整;
(3)若居民区有8000人,请估计爱唱歌的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
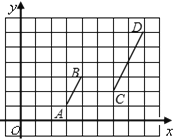
【题目】线段AB、CD在平面直角坐标系中位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(a、b),则直线OP与线段CD的交点坐标为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com