
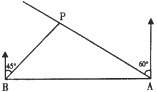
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
【答案】(1)6+6![]() (2)3+3
(2)3+3![]()
【解析】
(1)过点P作PD⊥AB于点D,先解Rt△PBD,得到BD和PD的长,再解Rt△PAD,得到AD和AP的长,然后根据BD+AD=AB,即可求解; (2)过点B作BF⊥AC于点F,解直角三角形即可得到结论.
(1)如图,过点P作PD⊥AB于点D.
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=6km.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
∴AD=![]() PD=6
PD=6![]() km,PA=12.
km,PA=12.
∴AB=BD+AD=(6+6![]() )km;
)km;
(2)如图,过点B作BF⊥AC于点F,
则∠BAP=30°,
∵AB=(6+6![]() ),
),
∴BF=![]() AB=(3+3
AB=(3+3![]() )km.
)km.
∴观测站B到射线AP的最短距离为(3+3![]() )km.
)km.


科目:初中数学 来源: 题型:
【题目】阅读材料:关于三角函数还有如下的公式:
Sin(α±β)=sinαcosβ±cosαsinβ ; tan(α±β)=![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值
例:tan15°=tan(45°30°)=![]() =
=![]()
根据以上阅读材料,请选择适当的公式答案下面的问题
(1)计算sin15°;
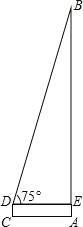
(2)栖灵塔是扬州市标志性建筑之一(如图),小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度.(精确到0.1米,参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
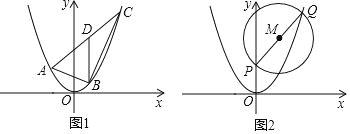
【题目】已知抛物线 ![]() :y=ax2 过点(2,2)
:y=ax2 过点(2,2)
(1)直接写出抛物线的解析式;
(2)如图,△ABC 的三个顶点都在抛物线![]() 上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求
上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求![]() 的值;
的值;
(3)如图,点 P 的坐标为(0,2),点 Q 为抛物线上![]() 上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( )
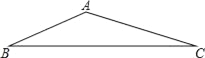
A. 450a元 B. 225a元 C. 150a元 D. 300a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,3)、点B(3,0),一次函数y=﹣2x的图象与直线AB交于点P.
(1)求P点的坐标.
(2)若点Q是x轴上一点,且△PQB的面积为6,求点Q的坐标.
(3)若直线y=﹣2x+m与△AOB三条边只有两个公共点,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)以O为中心作出△ABC的中心对称图形△A1B1C1,并写出点B1坐标;
(2)以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
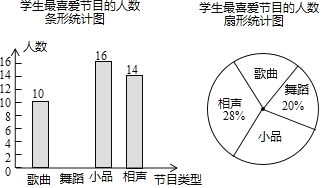
请你根据图中信息,回答下列问题:
(1)本次共调查了 名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于 度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为 人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣4=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为正整数,且该方程的两个根都是整数,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com