
【题目】已知抛物线 ![]() :y=ax2 过点(2,2)
:y=ax2 过点(2,2)
(1)直接写出抛物线的解析式;
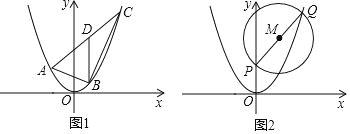
(2)如图,△ABC 的三个顶点都在抛物线![]() 上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求
上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求![]() 的值;
的值;
(3)如图,点 P 的坐标为(0,2),点 Q 为抛物线上![]() 上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)16;(3)见解析.
;(2)16;(3)见解析.
【解析】
(1)把点(2,2)坐标代入 y=ax2 即可求解;
(2)把 y=x+b 和 y=![]() x2 得:x2﹣2x﹣2b=0,设 A、C 两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1x2=﹣2b,可以求出点 D坐标、B坐标,即可求解;;
x2 得:x2﹣2x﹣2b=0,设 A、C 两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1x2=﹣2b,可以求出点 D坐标、B坐标,即可求解;;
(3)设点 Q坐标为(a,![]() a2),点 M的坐标为(
a2),点 M的坐标为(![]() ,
,![]() a2+1),圆的半径为 r,则 r2=
a2+1),圆的半径为 r,则 r2=![]() +(
+(![]() a2﹣1)2=
a2﹣1)2=![]() a4﹣
a4﹣![]() a2+1,点 M 到直线 y=t 的距离为 d, 用 HK=2
a2+1,点 M 到直线 y=t 的距离为 d, 用 HK=2![]() =2
=2![]() ,当
,当![]() =0时,HK为常数,t=
=0时,HK为常数,t=![]() ,HK=
,HK=![]() .
.
(1)把点(2,2)坐标代入y=ax2,解得:a=![]() ,
,
∴抛物线的解析式为y=x2;
(2)把y=x+b和y=![]() x2得:x2﹣2x﹣2b=0,
x2得:x2﹣2x﹣2b=0,
设A、C 两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1x2=﹣2b,
点D坐标为(![]() ,
,![]() ),即D(1,﹣b),B坐标为(1,
),即D(1,﹣b),B坐标为(1,![]() ),
),
AC2=[![]() (x2﹣x1)]2=16b+8,
(x2﹣x1)]2=16b+8,
BD=![]() +b,
+b,
∴![]() =16;
=16;
(3)设点Q坐标为(a,![]() a2),
a2),
点P的坐标为(0,2),由 P、Q坐标得点M的坐标为(![]() ,
,![]() a2+1),
a2+1),
设圆的半径为 r,由P(0,2)、M 两点坐标可得r2=![]() +(
+(![]() a2﹣1)2=
a2﹣1)2=![]() a4﹣
a4﹣![]() a2+1,
a2+1,
设点M到直线y=t的距离为d,则d2=(a2+1﹣t)=![]() a4+
a4+![]() a2+1+t2﹣2t﹣
a2+1+t2﹣2t﹣![]() a2t,
a2t,
则 HK=2![]() =2
=2![]() ,
,
当![]() =0 时,HK为常数,t=
=0 时,HK为常数,t=![]() ,
,
HK=![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
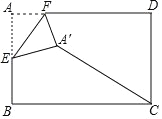
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机可以通过“个人热点”功能实现移动网络共享,小明和小亮准备到操场上测试个人热点连接的有效距离,他们从相距![]() 的
的![]() ,
,![]() 两地相向而行.图中
两地相向而行.图中![]() ,
,![]() 分别表示小明、小亮两人离
分别表示小明、小亮两人离![]() 地的距离
地的距离![]() 与步行时间
与步行时间![]() 之间的函数关系,其中
之间的函数关系,其中![]() 的关系式为
的关系式为![]() .根据图象回答下列问题:
.根据图象回答下列问题:

(1)请写出![]() 的关系式___________;
的关系式___________;
(2)小明和小亮出发后经过了多长时间相遇?
(3)如果手机个人热点连接的有效距离不超过![]() ,那么他们出发多长时间才能连接成功?连接持续了多长时间?
,那么他们出发多长时间才能连接成功?连接持续了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
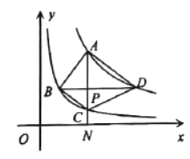
【题目】如图,四边形![]() 在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数
在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数![]() 与
与![]() 的图象上,对角线
的图象上,对角线![]() 于点
于点![]() ,
,![]() 轴于点
轴于点![]() .
.
(1)若![]() ,试求
,试求![]() 的值;
的值;
(2)当![]() ,点
,点![]() 是线段
是线段![]() 的中点时,试判断四边形
的中点时,试判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
(3)直线![]() 与
与![]() 轴相交于
轴相交于![]() 点.当四边形
点.当四边形![]() 为正方形时,请求出
为正方形时,请求出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠ABC=60°,BC=8,点 D 是 BC 边的中点,点 E 是边 AC上一点,过点 D 作 ED 的垂线交边 AC 于点 F,若 AC=7CF,且 DE 恰好平分△ABC 的周长,则△ABC 的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)面“学”的对面是面什么?
(2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
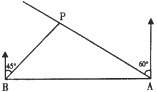
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
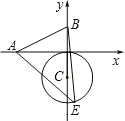
【题目】如图,已知 A、B 两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为 1,E 是⊙C 上的一动点,则△ABE 面积的最大值为( )
A. ![]() B. 3+
B. 3+![]() C. 3+
C. 3+![]() D. 4+
D. 4+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在七年级设立了六个课外兴趣小组,每个参加者只能参加一个兴趣小组,下面是六个兴趣小组不完整的频数分布直方图和扇形统计图.根据图中信息,解决下列问题:

(1)七年级共有 人参加了兴趣小组;
(2)体育兴趣小组对应扇形圆心角的度数为 ;
(3)以各小组人数组成一组新数据,求这组新数据的中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com