
【题目】手机可以通过“个人热点”功能实现移动网络共享,小明和小亮准备到操场上测试个人热点连接的有效距离,他们从相距![]() 的
的![]() ,
,![]() 两地相向而行.图中
两地相向而行.图中![]() ,
,![]() 分别表示小明、小亮两人离
分别表示小明、小亮两人离![]() 地的距离
地的距离![]() 与步行时间
与步行时间![]() 之间的函数关系,其中
之间的函数关系,其中![]() 的关系式为
的关系式为![]() .根据图象回答下列问题:
.根据图象回答下列问题:

(1)请写出![]() 的关系式___________;
的关系式___________;
(2)小明和小亮出发后经过了多长时间相遇?
(3)如果手机个人热点连接的有效距离不超过![]() ,那么他们出发多长时间才能连接成功?连接持续了多长时间?
,那么他们出发多长时间才能连接成功?连接持续了多长时间?
【答案】(1)![]() ;(2)经过
;(2)经过![]() 后二者相遇;(3)出发
后二者相遇;(3)出发![]() 时才能连接,持续了
时才能连接,持续了![]()
【解析】
(1) 设![]() 的解析式为y=kx,把(100,100)代入求解即可;
的解析式为y=kx,把(100,100)代入求解即可;
(2)把函数解析式联立方程组,求得方程组的解即可;
(3) 设当出发![]()
![]() 时相距
时相距![]() ,小亮速度为
,小亮速度为![]() ,得出
,得出![]() ,求解即可得出出发32s才能连接成功;再求出t=48s连接断开,即可求出持续的时间.
,求解即可得出出发32s才能连接成功;再求出t=48s连接断开,即可求出持续的时间.
解:(1)设![]() 的解析式为y=kx,
的解析式为y=kx,
把(100,100)代入得,100=100k,
∴k=1
∴![]() .
.
故答案为y=x.
(2)由题意得![]()
解得![]()
![]() 经过
经过![]() 后二者相遇.
后二者相遇.
(3)解:设当出发![]()
![]() 时相距
时相距![]() ,
,
由题知,小亮速度为![]() .
.
![]()
解得![]() ,
,
∴他们出发32s才能连接成功;
当![]()
解得![]() ,即t=48s连接断开,
,即t=48s连接断开,
故连接了![]()
![]() 出发
出发![]() 时才能连接,持续了
时才能连接,持续了![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:关于三角函数还有如下的公式:
Sin(α±β)=sinαcosβ±cosαsinβ ; tan(α±β)=![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值
例:tan15°=tan(45°30°)=![]() =
=![]()
根据以上阅读材料,请选择适当的公式答案下面的问题
(1)计算sin15°;
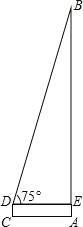
(2)栖灵塔是扬州市标志性建筑之一(如图),小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度.(精确到0.1米,参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
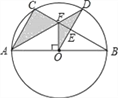
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2![]() .
.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
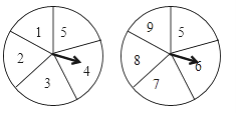
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划组织员工外出甲、乙旅行社的服务质量相问,且对外报价都是300元/人,该公司联系时,甲旅行社表示可给每人八折优惠;乙旅行社表示可免去一人的费用,其余人九折优惠.
(1)根据题意,填写下表:
外出人数(人) | 10 | 11 |
甲旅行社收费(元) | ____ | 2640 |
乙旅行社收费(元) | 2430 | ____ |
(2)设该公司此次外出有![]() 人,选择甲旅行社的费用为
人,选择甲旅行社的费用为![]() 元,选择乙旅行社的费用为
元,选择乙旅行社的费用为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数关系式
的函数关系式
(3)该公司外出人数在什么范围内,选甲旅行社划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 ![]() :y=ax2 过点(2,2)
:y=ax2 过点(2,2)
(1)直接写出抛物线的解析式;
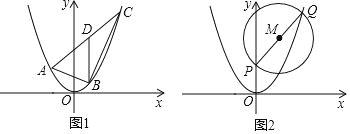
(2)如图,△ABC 的三个顶点都在抛物线![]() 上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求
上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求![]() 的值;
的值;
(3)如图,点 P 的坐标为(0,2),点 Q 为抛物线上![]() 上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
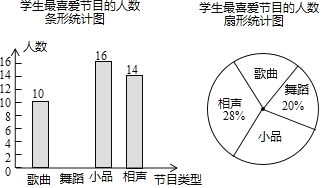
请你根据图中信息,回答下列问题:
(1)本次共调查了 名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于 度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为 人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com