
【题目】阅读材料:关于三角函数还有如下的公式:
Sin(α±β)=sinαcosβ±cosαsinβ ; tan(α±β)=![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值
例:tan15°=tan(45°30°)=![]() =
=![]()
根据以上阅读材料,请选择适当的公式答案下面的问题
(1)计算sin15°;
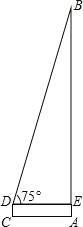
(2)栖灵塔是扬州市标志性建筑之一(如图),小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度.(精确到0.1米,参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
【答案】(1)![]() ;(2)信号塔AB的高度约为27.7米
;(2)信号塔AB的高度约为27.7米
【解析】
(1)把15°化为45°-30°以后,再利用公式sin(α±β)=sinαcosβ±cosasinβ计算,即可求出sin15°的值;
(2)先根据锐角三角函数的定义求出BE的长,再根据AB=AE+BE即可得出结论.
(1)sin15°=sin(45°30°)=sin45°cos30°cos45°sin30°=![]()
(2)在RT△BDE中,DE=AC=7,
∠BDE=75°,
tan∠BDE=BEDE,
∴BE=DEtan∠BDE=DEtan75°,
∵tan75°=tan(45°+30°)=![]() =
=![]()
∴BE=7(![]() )≈26.12,
)≈26.12,
∴信号塔AB的高度≈26.12+1.62≈27.7(米),
答:该信号塔AB的高度约为27.7米.


科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)求证:四边形![]() 为矩形;
为矩形;
(2)判断四边形![]() 是什么特殊四边形?并说明理由;
是什么特殊四边形?并说明理由;
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
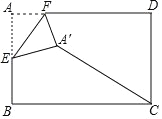
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张规格、质地相同的卡片,它们背面完全相同,正面图案分别是A 菱形,B 平行四边形,C 线段,D 角,将这四张卡片背面朝上洗匀后
(1)随机抽取一张卡片图案是轴对称图形的概率是 ;
(2)随机抽取两张卡片(不放回),求两张卡片卡片图案都是中心对称图形的概率,并用树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若圆的一条弦把圆分成度数比为1:4的两段弧,则弦所对的圆周角等于( )
A. 36° B. 72° C. 36°或144° D. 72°或108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机可以通过“个人热点”功能实现移动网络共享,小明和小亮准备到操场上测试个人热点连接的有效距离,他们从相距![]() 的
的![]() ,
,![]() 两地相向而行.图中
两地相向而行.图中![]() ,
,![]() 分别表示小明、小亮两人离
分别表示小明、小亮两人离![]() 地的距离
地的距离![]() 与步行时间
与步行时间![]() 之间的函数关系,其中
之间的函数关系,其中![]() 的关系式为
的关系式为![]() .根据图象回答下列问题:
.根据图象回答下列问题:

(1)请写出![]() 的关系式___________;
的关系式___________;
(2)小明和小亮出发后经过了多长时间相遇?
(3)如果手机个人热点连接的有效距离不超过![]() ,那么他们出发多长时间才能连接成功?连接持续了多长时间?
,那么他们出发多长时间才能连接成功?连接持续了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
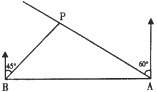
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com