
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)求证:四边形![]() 为矩形;
为矩形;
(2)判断四边形![]() 是什么特殊四边形?并说明理由;
是什么特殊四边形?并说明理由;
(3)求四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)四边形EFPH为矩形,理由见解析;(3)![]()
【解析】
(1)由平行线的性质证出∠BCD=90°即可;
(2)根据矩形性质得出CD=2,根据勾股定理求出CE和BE,求出CE2+BE2的值,求出BC2,根据勾股定理的逆定理求出∠BEC=90°,根据矩形的性质和平行四边形的判定,推出平行四边形DEBP和AECP,推出EH//FP,EF//HP,推出平行四边形EFPH,根据矩形的判定推出即可;
(3)根据三角形的面积公式求出CF,求出EF,根据勾股定理求出PF,根据面积公式求出即可.
(1)证明:∵AB//CD,
∴∠CBA+∠BCD=180°,
∵∠CBA=∠ADC=90°,
∴∠BCD=90°,
∴四边形ABCD是矩形;
(2)解:四边形EFPH为矩形;理由如下:
∵四边形ABCD是矩形,
∴AD=BC=5,AB=CD=2,AD∥BC,
由勾股定理得:CE= ![]() ,
,
同理BE=2![]() ,
,
∴CE2+BE2=5+20=25,
∵BC2=52=25,
∴BE2+CE2=BC2,
∴∠BEC=90°,
∴△BEC是直角三角形.
∵DE=BP,DE//BP,
∴四边形DEBP是平行四边形,
∴BE//DP,
∵AD=BC,AD//BC,DE=BP,
∴AE=CP,
∴四边形AECP是平行四边形,
∴AP//CE,
∴四边形EFPH是平行四边形,
∵∠BEC=90°,
∴平行四边形EFPH是矩形.
(3)解:∵四边形AECP是平行四边形,
∴PD=BE=2![]() ,
,
在Rt△PCD中,FC⊥PD,PC=BC-BP=4,
由三角形的面积公式得:![]() PDCF=
PDCF=![]() PCCD,
PCCD,
∴CF=![]() ,
,
∴EF=CE-CF=![]() ,
,
∵PF=![]() ,
,
∴S矩形EFPH=EFPF=![]() ,
,
即:四边形EFPH的面积是![]() .
.


科目:初中数学 来源: 题型:
【题目】近日,中国工程院院士、“杂交水稻之父”袁隆平团队选育培植的耐盐碱水稻(即海水稻)在山东青岛等六个试验基地开始春播育秧,预计今年的种植规模将超一万亩.已知去年某基地甲、乙两块实验田海水稻的总产量都是3600千克,乙实验田海水稻种植面积是甲实验田的![]() ,而乙实验田海水稻平均亩产量比甲多60千克.
,而乙实验田海水稻平均亩产量比甲多60千克.
(1)求甲、乙两块实验田种植海水稻的面积;
(2)经过科学家的努力,海水稻正从试验田走向餐桌,某电商新购进A、B两种包装的海水稻产品共50袋,其进价、标价及优惠方案如下表所示.若要保证这批海水稻产品全部售出后所得利润不少于1000元,该电商至少要购进A种包装的海水稻产品多少袋?
包装类型 | A | B |
进价(元/袋) | 100 | 30 |
标价(元/袋) | 150 | 50 |
优惠方案 | 全部九折 | |
查看答案和解析>>
科目:初中数学 来源: 题型:
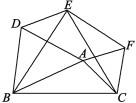
【题目】如图,已知△ABC,点A在BC边的上方,把△ABC绕点B逆时针方向旋转60°得△DBE,绕点C顺时针方向旋转60°得△FEC,连接AD,AF.
(1)△ABD,△ACF,△BCE是什么特殊三角形?请说明理由;
(2)当△ABC满足什么条件时,四边形ADEF是正方形?请说明理由;
(3)当△ABC满足什么条件时,以点A,D,E,F为顶点的四边形不存在?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
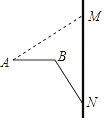
【题目】高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN=75cm,且可以看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
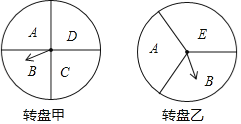
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级物理兴趣小组20位同学在实验操作中的得分如表:
得分(分) | 10 | 9 | 8 | 7 |
人数(人) | 5 | 8 | 4 | 3 |
(1)求这20位同学实验操作得分的众数,中位数;
(2)这20位同学实验操作得分的平均分是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
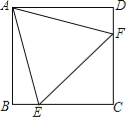
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=![]() .
.
其中正确的序号是 (把你认为正确的都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:关于三角函数还有如下的公式:
Sin(α±β)=sinαcosβ±cosαsinβ ; tan(α±β)=![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值
例:tan15°=tan(45°30°)=![]() =
=![]()
根据以上阅读材料,请选择适当的公式答案下面的问题
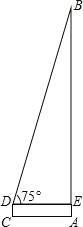
(1)计算sin15°;
(2)栖灵塔是扬州市标志性建筑之一(如图),小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度.(精确到0.1米,参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com