
【题目】在![]() ,
,![]() ,
,![]() ,高
,高![]() ,则BC的长是( )
,则BC的长是( )
A.14B.4C.4或14D.7或13
【答案】C
【解析】
分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CDBD.
解:(1)如图
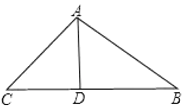
锐角△ABC中,AB=15,AC=13,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2AD2=152122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得
CD2=AC2AD2=132122=25,
∴CD=5,
∴BC的长为BD+DC=9+5=14;
(2)如图
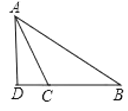
钝角△ABC中,AB=15,AC=13,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2AD2=152122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得:
CD2=AC2AD2=132122=25,
∴CD=5,
∴BC的长为DCBD=95=4.
故BC长为14或4.
故选:C.


科目:初中数学 来源: 题型:
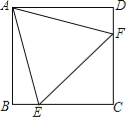
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=![]() .
.
其中正确的序号是 (把你认为正确的都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
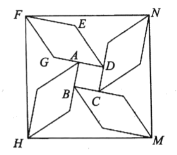
【题目】如图,正方形![]() 面积为
面积为![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() ,以
,以![]() 为边在正方形另一侧作菱形
为边在正方形另一侧作菱形![]() ,其中
,其中![]() ,依次延长
,依次延长![]() 类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点
类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点![]() 则四边形
则四边形![]() 的面积为___________.
的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:关于三角函数还有如下的公式:
Sin(α±β)=sinαcosβ±cosαsinβ ; tan(α±β)=![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值
例:tan15°=tan(45°30°)=![]() =
=![]()
根据以上阅读材料,请选择适当的公式答案下面的问题
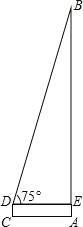
(1)计算sin15°;
(2)栖灵塔是扬州市标志性建筑之一(如图),小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度.(精确到0.1米,参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
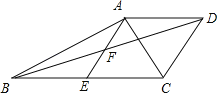
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
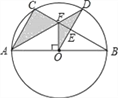
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2![]() .
.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
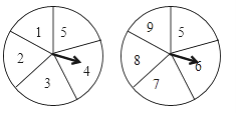
【题目】如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)以O为中心作出△ABC的中心对称图形△A1B1C1,并写出点B1坐标;
(2)以格点P为旋转中心,将△ABC按顺时针方向旋转90°,得到△A′B′C′,且使点A的对应点A′的恰好落在△A1B1C1的内部格点上(不含△A1B1C1的边上),写出点P的坐标,并画出旋转后的△A′B′C′.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com