
【题目】如图,正方形![]() 面积为
面积为![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() ,以
,以![]() 为边在正方形另一侧作菱形
为边在正方形另一侧作菱形![]() ,其中
,其中![]() ,依次延长
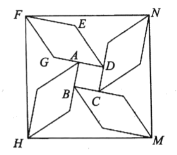
,依次延长![]() 类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点
类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点![]() 则四边形
则四边形![]() 的面积为___________.
的面积为___________.
【答案】![]()
【解析】
如图所示,延长CD交FN于点P,过N作NK⊥CD于点K,延长FE交CD于点Q,交NS于点R,首先利用正方形性质结合题意求出AD=CD=AG=DQ=1,然后进一步根据菱形性质得出DE=EF=DG=2,再后通过证明四边形NKQR是矩形得出QR=NK=![]() ,进一步可得
,进一步可得![]() ,再延长NS交ML于点Z,利用全等三角形性质与判定证明四边形FHMN为正方形,最后进一步求解即可.
,再延长NS交ML于点Z,利用全等三角形性质与判定证明四边形FHMN为正方形,最后进一步求解即可.

如图所示,延长CD交FN于点P,过N作NK⊥CD于点K,延长FE交CD于点Q,交NS于点R,
∵ABCD为正方形,
∴∠CDG=∠GDK=90°,
∵正方形ABCD面积为1,
∴AD=CD=AG=DQ=1,
∴DG=CT=2,
∵四边形DEFG为菱形,
∴DE=EF=DG=2,
同理可得:CT=TN=2,
∵∠EFG=45°,
∴∠EDG=∠SCT=∠NTK=45°,
∵FE∥DG,CT∥SN,DG⊥CT,
∴∠FQP=∠FRN=∠DQE=∠NKT=90°,
∴DQ=EQ=TK=NK=![]() ,FQ=FE+EQ=
,FQ=FE+EQ=![]() ,
,
∵∠NKT=∠KQR=∠FRN=90°,
∴四边形NKQR是矩形,
∴QR=NK=![]() ,
,
∴FR=FQ+QR=![]() ,NR=KQ=DKDQ=
,NR=KQ=DKDQ=![]() ,
,
∴![]() ,
,
再延长NS交ML于点Z,易证得:△NMZ△FNR(SAS),
∴FN=MN,∠NFR=∠MNZ,
∵∠NFR+∠FNR=90°,
∴∠MNZ+∠FNR=90°,
即∠FNM=90°,
同理可得:∠NFH=∠FHM=90°,
∴四边形FHMN为正方形,
∴正方形FHMN的面积=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
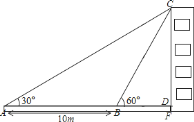
【题目】如图,某教学兴趣小组想测量某建筑物的高度,他们在A点测得屋顶C的仰角为30°,然后沿AD方向前进10米,到达B点,在B点测得屋顶C的仰角为60°,已知测量仪AE的高度为1米,请你根据他们的测量数据计算建筑物CF的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
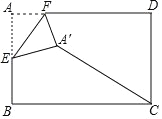
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张规格、质地相同的卡片,它们背面完全相同,正面图案分别是A 菱形,B 平行四边形,C 线段,D 角,将这四张卡片背面朝上洗匀后
(1)随机抽取一张卡片图案是轴对称图形的概率是 ;
(2)随机抽取两张卡片(不放回),求两张卡片卡片图案都是中心对称图形的概率,并用树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠ABC=60°,BC=8,点 D 是 BC 边的中点,点 E 是边 AC上一点,过点 D 作 ED 的垂线交边 AC 于点 F,若 AC=7CF,且 DE 恰好平分△ABC 的周长,则△ABC 的面积为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com