
【题目】如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°.求BC的长和四边形ABCD的面积.
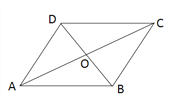
【答案】BC的长为12,四边形ABCD的面积为120
【解析】试题分析:根据勾股定理求得OA的长,再根据对角线互相平分的四边形是平行四边形证明四边形ABCD是平行四边形,从而根据平行四边形的对边相等就可求得BC的长;根据平行四边形的面积公式可以求得它的面积.
试题解析:在△AOD中,∠ADB=90°,AD=12,0D=5,
根据勾股定理,得
OA2=OD2+AD2=52+122=169,
∴OA=13.
∵AC=26,OA=13,
∴OA=OC,
又DO=OB,
∴四边形ABCD为平行四边形,
∴AD=BC=12;
∵∠ADB=90°,
∴AD⊥BD,
∴S四边形ABCD=ADBD=12×10=120,
答:BC的长为12,四边形ABCD的面积为120.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/s的速度向点D匀速运动.设点P的运动时间为ts,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家体育用品商店出售同样的乒乓球和乒乓拍,乒乓球拍每幅定价20元,乒乓球每盒定价5元,现两家商店搞促销活动.甲店:每买一副球拍送一盒乒乓球;乙店:按定价的8折优惠.某班级需购球拍4副,乒乓球若干盒(不少于4盒).
(1)设购买乒乓球盒数为![]() (盒),在甲店购买的付款数为
(盒),在甲店购买的付款数为![]() (元);在乙店购买的付款数为
(元);在乙店购买的付款数为![]() (元),分别写出
(元),分别写出![]() 和
和![]() 与
与![]() 的函数关系式,并写出定义域.
的函数关系式,并写出定义域.
(2)就乒乓球的盒数讨论去哪家购买合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p= ,且其日销售量y(kg)与时间t(天)的关系如表:
,且其日销售量y(kg)与时间t(天)的关系如表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
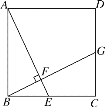
【题目】如图,在正方形ABCD中,点E在边BC上(点E不与点B重合),连接AE,过点B作BF⊥AE于点F,交CD于点G.
(1)求证:△ABF∽△BGC;
(2)若AB=2,G是CD的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 面积为
面积为![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() ,以
,以![]() 为边在正方形另一侧作菱形
为边在正方形另一侧作菱形![]() ,其中
,其中![]() ,依次延长
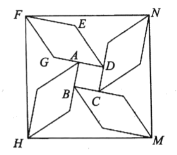
,依次延长![]() 类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点
类似以上操作再作三个形状大小都相同的菱形,形成风车状图形,依次连结点![]() 则四边形
则四边形![]() 的面积为___________.
的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)

查看答案和解析>>
科目:初中数学 来源: 题型:
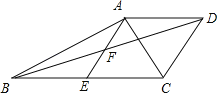
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com