
ЁОЬтФПЁПЩЬУГЙЋЫОЙКНјФГжжЫЎЙћЕФГЩБОЮЊ20дЊ/kgЃЌОЙ§ЪаГЁЕїбаЗЂЯжЃЌетжжЫЎЙћдкЮДРД48ЬьЕФЯњЪлЕЅМлpЃЈдЊ/kgЃЉгыЪБМфtЃЈЬьЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊp= ЃЌЧвЦфШеЯњЪлСПyЃЈkgЃЉгыЪБМфtЃЈЬьЃЉЕФЙиЯЕШчБэЃК
ЃЌЧвЦфШеЯњЪлСПyЃЈkgЃЉгыЪБМфtЃЈЬьЃЉЕФЙиЯЕШчБэЃК
ЪБМфtЃЈЬьЃЉ | 1 | 3 | 6 | 10 | 20 | 40 | Ё |
ШеЯњЪлСПyЃЈkgЃЉ | 118 | 114 | 108 | 100 | 80 | 40 | Ё |
ЃЈ1ЃЉвбжЊyгыtжЎМфЕФБфЛЏЙцТЩЗћКЯвЛДЮКЏЪ§ЙиЯЕЃЌЪдЧѓдкЕк30ЬьЕФШеЯњЪлСПЪЧЖрЩйЃП
ЃЈ2ЃЉЮЪФФвЛЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓШеЯњЪлРћШѓЮЊЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉy=Љ2t+120ЃЛдкЕк30ЬьЕФШеЯњЪлСПЪЧ60kgЃЈ2ЃЉЕБt=10ЪБЃЌWзюДѓ=1250дЊ
ЁОНтЮіЁПЪдЬтЗжЮі:ЃЈ1ЃЉЩшy=kt+bЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉШеРћШѓ=ШеЯњЪлСПЁСУПЙЋНяРћШѓЃЌОнДЫЗжБ№БэЪОЧА24ЬьКЭКѓ24ЬьЕФШеРћШѓЃЌИљОнКЏЪ§аджЪЧѓзюДѓжЕКѓБШНЯЕУНсТлЃЎ
ЃЈ1ЃЉЩшy=kt+bЃЌАбt=1ЃЌy=118ЃЛt=3ЃЌy=114ДњШыЕУЕНЃК
![]()
НтЕУ![]() ЃЌ
ЃЌ
Ёрy=Љ2t+120ЃЎ
НЋt=30ДњШыЩЯЪНЃЌЕУЃКy=Љ2ЁС30+120=60ЃЎ
ЫљвддкЕк30ЬьЕФШеЯњЪлСПЪЧ60kgЃЎ
ЃЈ2ЃЉЩшРћШѓЮЊWдЊ
ЕБ1ЁмtЁм14ЪБЃЌW=ЃЈpЉ20ЃЉy=Љ![]() t2+10t+1200=Љ
t2+10t+1200=Љ![]() ЃЈtЉ10ЃЉ2+1250ЃЌ
ЃЈtЉ10ЃЉ2+1250ЃЌ
ЕБt=10ЪБЃЌWзюДѓ=1250дЊ
ЕБ25ЁмtЁм48ЪБЃЌW=ЃЈpЉ20ЃЉy=t2Љ116t+3360=ЃЈtЉ58ЃЉ2Љ4ЃЌ
ЕБt=25ЪБЃЌWзюДѓ=1085дЊ
Ёп1250ЃО1085ЃЌ
ЁрзлЩЯЃЌЕБt=10ЪБЃЌWзюДѓ=1250дЊЃЎ
ЕуОІ: БОЬтжївЊПМВщвЛДЮКЏЪ§КЭЖўДЮКЏЪ§ЕФгІгУЃЌУїШЗЦфжаЕФЪ§СПЙиЯЕЪЧНтЬтЕФЙиМќЃЛЖўДЮКЏЪ§ЧѓзюжЕЕФГЃгУЗНЗЈЪЧАбКЏЪ§ЕФвЛАуЪНЪНЭЈЙ§ХфЗНЛЏЮЊЖЅЕуЪН,ДгЖјИљОнЖўДЮКЏЪ§ЕФаджЪПЩЧѓГізюжЕ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌгаЕу![]() .
.
ЃЈ1ЃЉШєЯпЖЮ![]() жсЃЌЧѓЕу
жсЃЌЧѓЕу![]() ЕФзјБъ
ЕФзјБъ
ЃЈ2ЃЉЕБЕу![]() ЕН
ЕН![]() жсЕФОрРыЪЧЕН
жсЕФОрРыЪЧЕН![]() жсЕФОрРыЕФ
жсЕФОрРыЕФ![]() БЖЪБЃЌЧѓЕу
БЖЪБЃЌЧѓЕу![]() ЫљдкЕФЯѓЯоЮЛжУ
ЫљдкЕФЯѓЯоЮЛжУ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
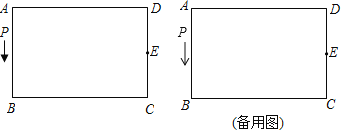
ЁОЬтФПЁПШчЭМ,НЋГЄЗНаЮжНЦЌЕФвЛНЧзїелЕўЃЌЪЙЖЅЕу A Тфдк AДІ, DE ЮЊелКлЃЌНЋ BEAЖделЃЌЪЙЕУ BТфдкжБЯп EAЩЯЃЌЕУелКл EG .
(1)Чѓ DEG ЕФЖШЪ§ЃЛ
(2) Шє EAЧЁКУЦНЗж DEB ЃЌЧѓ DEAЕФЖШЪ§ .

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтЁАПЮГЬбЁаоЁБЕФЧщПіЃЌЖдБЈУћВЮМгЁАвеЪѕМјЩЭЁБЁЂЁАПЦММжЦзїЁБЁЂЁАЪ§бЇЫМЮЌЁБЁЂЁАдФЖСаДзїЁБетЫФИібЁаоЯюФПЕФбЇЩњЃЈУПШЫЯоБЈвЛЯюЃЉНјааГщбљЕїВщЃЌЯТУцЪЧИљОнЪеМЏЕФЪ§ОнЛцжЦЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉДЫДЮЙВЕїВщСЫЁЁ ЁЁУћбЇЩњЃЌЩШаЮЭГМЦЭМжаЃЌЁАвеЪѕМјЩЭЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЪЧЁЁ ЁЁЖШЃЛ
ЃЈ2ЃЉЧыАбетИіЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЯжИУаЃ700УћбЇЩњБЈУћВЮМгетЫФИібЁаоЯюФПЃЌЧыФуЙРМЦгаЖрЩйУћбЇЩњВЮМгСЫЁАЪ§бЇЫМЮЌЁБЯюФПЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩљвєдкПеЦјжаЕФДЋВЅЫйЖШyЃЈm/sЃЉЫцЦјЮТxЃЈЁцЃЉЕФБфЛЏЖјБфЛЏ.ЯТБэИјГіСЫвЛзщВЛЭЌЦјЮТЯТЩљвєДЋВЅЕФЫйЖШЃК
xЃЈЁцЃЉ | 0 | 5 | 10 | 15 | 20 | 25 |
yЃЈm/sЃЉ | 331 | 334 | 337 | 340 | 343 | 346 |
ЃЈ1ЃЉЕБxЕФжЕЮЊ35ЪБЃЌЧѓЖдгІЕФyЕФжЕЃЛ
ЃЈ2ЃЉЧѓyгыxЕФЙиЯЕЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЮЊЁЯEACЕФНЧЦНЗжЯпЃЌDEЁЭAEЃЌDFЁЭACЃЌЁЯEBD=ЁЯFCD.

ЃЈ1ЃЉХаЖЯЁїBDCЕФаЮзДВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧѓжЄЃКCF-AF=AB.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊГЄЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() БпЕФжаЕуЃЌ
БпЕФжаЕуЃЌ![]() ЮЊГЄЗНаЮ
ЮЊГЄЗНаЮ![]() БпЩЯЕФЖЏЕуЃЌЖЏЕу
БпЩЯЕФЖЏЕуЃЌЖЏЕу![]() вд
вд![]() ИіЕЅЮЛ/УыЕФЫйЖШДг
ИіЕЅЮЛ/УыЕФЫйЖШДг![]() ГіЗЂЃЌбизХ
ГіЗЂЃЌбизХ![]() дЫЖЏЕН
дЫЖЏЕН![]() ЕуЭЃжЙЃЌЩшЕу
ЕуЭЃжЙЃЌЩшЕу![]() дЫЖЏЕФЪБМфЮЊ
дЫЖЏЕФЪБМфЮЊ![]() УыЃЌ
УыЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЁЃ
ЁЃ
ЃЈ1ЃЉЧѓЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕЪЧ________ЃЛЕБ
ЕФжЕЪЧ________ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФжЕЪЧ________.
ЕФжЕЪЧ________.
ЃЈ2ЃЉЕБЕу![]() дк
дк![]() ЩЯЪБЃЌЧѓГі
ЩЯЪБЃЌЧѓГі![]() гы
гы![]() жЎМфЕФЙиЯЕЪНЃЛ
жЎМфЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯдЫЖЏЕНФГвЛЪБПЬЪБЃЌ
ЩЯдЫЖЏЕНФГвЛЪБПЬЪБЃЌ![]() ЕФжмГЄзюаЁЪБЃЌЧѓДЫЪБ
ЕФжмГЄзюаЁЪБЃЌЧѓДЫЪБ![]() ЕФЖШЪ§.
ЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаоРэГЇашвЊЙКНјМзЁЂввСНжжХфМўЃЌОЕїВщЃЌУПИіМзжжХфМўЕФМлИёБШУПИіввжжХфМўЕФМлИёЩй0.4ЭђдЊЃЌЧвгУ16ЭђдЊЙКТђЕФМзжжХфМўЕФЪ§СПгыгУ24ЭђдЊЙКТђЕФввжжХфМўЕФЪ§СПЯрЭЌЃЎ
ЃЈ1ЃЉЧѓУПИіМзжжХфМўЁЂУПИіввжжХфМўЕФМлИёЗжБ№ЮЊЖрЩйЭђдЊЃЛ
ЃЈ2ЃЉЯжЭЖШызЪН№40ЭђдЊЃЌИљОнЮЌаоашвЊдЄВтЃЌМзжжХфМўвЊБШввжжХфМўжСЩйвЊЖр11МўЃЌЮЪввжжХфМўзюЖрПЩЙКТђЖрЩйМўЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com