
【题目】如图,已知长方形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,
边的中点,![]() 为长方形
为长方形![]() 边上的动点,动点
边上的动点,动点![]() 以
以![]() 个单位/秒的速度从
个单位/秒的速度从![]() 出发,沿着
出发,沿着![]() 运动到
运动到![]() 点停止,设点
点停止,设点![]() 运动的时间为
运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() 。
。
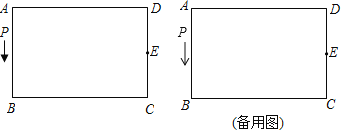
(1)求当![]() 时,
时,![]() 的值是________;当
的值是________;当![]() 时,
时,![]() 的值是________.
的值是________.
(2)当点![]() 在
在![]() 上时,求出
上时,求出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)当![]() 在线段
在线段![]() 上运动到某一时刻时,
上运动到某一时刻时,![]() 的周长最小时,求此时
的周长最小时,求此时![]() 的度数.
的度数.
【答案】(1)96,160;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)当t=2时,判断出点P在AB上,利用三角形的面积公式得出结论;当t=6时,判断出点P在BC上,由长方形面积减去3个直角三角形的面积,即可得出结论;
(2)由长方形减去3个直角三角形的面积,即可得出结论;
(3)判断出点P的位置,即可得出结论.
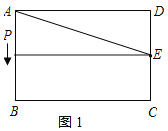
解:(1)长方形ABCD中,AB=CD=16,BC=DA=24,AD∥BC,∠BAD=∠B=∠C=∠D=90°,
∵P以4个单位/秒的速度从A出发,沿着A→B→C→E运动到E点停止,
∴当t=2时,则AP=4×2=8=![]() AB,
AB,
即P为AB的中点,
∵E为CD边的中点,
∴四边形APED是矩形,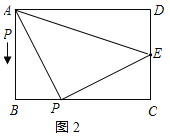
∴CE=DE=8,∠APE=∠B=90°,PE⊥AB,PE=BC=24,
∴△APE的面积为y=![]() ×24×8=96;
×24×8=96;
当t=6时,BP=6×4-AB=24-16=8,
∴PC=BC-BP=16,
∴△APE的面积为y=24×16-![]() ×16×8-
×16×8-![]() ×16×8-
×16×8-![]() ×24×8=160;
×24×8=160;
故答案为:96;160;
(2)当点P在BC上时,BP=4t-16,
则PC=24-(4t-16)=40-4t,
∴y=24×16-![]() ×16×(4t-16)-
×16×(4t-16)-![]() ×(40-4t)×8-
×(40-4t)×8-![]() ×24×8=-16t+256,
×24×8=-16t+256,
∴y与t之间的关系式为y=-16t+256;
(3)如图3,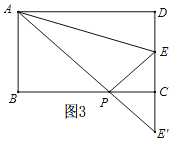
延长EC到E',使得E'C=EC,连接AE',交BC于点P.
此时△APE周长最短;
∵EC=CE'=8,
∴EE'=16,DE'=24=AD,
∴AE'=![]() AD=24
AD=24![]() ,
,
∵PC⊥EE'且平分EE',
∴PE=PE',
∴AP+PE=24![]() ,∵AD=,24,DE=8,
,∵AD=,24,DE=8,
∴AE=![]() =8
=8![]() ,
,
∴△APE的周长最小值=24![]() +8
+8![]() ;
;
在Rt△ADE'中,∵AD=DE',∠D=90°,
∴△ADE'是等腰直角三角形,
∴∠DAE'=45°,
∴∠PAB=45°.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】有若干个仅颜色不同的红球和黑球,现往一个不透明的袋子里装进4个红球和6个黑球.
(1)若先从袋子里取出m个红球(不放回),再从袋子里随机摸出一个球,将“摸到黑球”记为事件A. 若事件A为必然事件,则m= .
(2)若先从袋子里取出n个黑球,再放入2n个红球,若随机摸出一个球是红球的概率等于2/3,通过计算求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H.且点C是![]() 的中点,若扇形的半径为3.则图中阴影部分的面积等于______.
的中点,若扇形的半径为3.则图中阴影部分的面积等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p= ,且其日销售量y(kg)与时间t(天)的关系如表:
,且其日销售量y(kg)与时间t(天)的关系如表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小梅骑自行车去外婆家,从家出发![]() 小时后到达甲地,在甲地游玩一段时间后,按原速继续前进,小梅出发
小时后到达甲地,在甲地游玩一段时间后,按原速继续前进,小梅出发![]() 小时后,爸爸骑摩托车沿小梅骑自行车的路线追赶小梅,如图是他们离家的路程
小时后,爸爸骑摩托车沿小梅骑自行车的路线追赶小梅,如图是他们离家的路程![]() (千米)与小梅离家时间
(千米)与小梅离家时间![]() (小时)的关系图,已知爸爸骑摩托车的速度是小梅骑自行车速度的
(小时)的关系图,已知爸爸骑摩托车的速度是小梅骑自行车速度的![]() 倍。
倍。
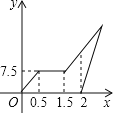
(1)小梅在甲地游玩时间是_________小时,小梅骑车的速度是_________千米/小时.
(2)若爸爸与小梅同时到达外婆家,求小梅家到外婆家的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条笔直的公路上顺次有![]() 三地,小军早晨
三地,小军早晨![]() 从
从![]() 地出发沿这条公路骑自行车前往
地出发沿这条公路骑自行车前往![]() 地,同时小林从
地,同时小林从![]() 地出发沿这条公路骑摩托车前往
地出发沿这条公路骑摩托车前往![]() 地,小林到地后休息了
地,小林到地后休息了 ![]() 个小时, 然后掉头原路原速返回追赶小军,经过一段时间后两人同时到达
个小时, 然后掉头原路原速返回追赶小军,经过一段时间后两人同时到达![]() 地,设两人行驶的时间为
地,设两人行驶的时间为![]() (小时),两人之间的距离为
(小时),两人之间的距离为![]() (千米),
(千米), ![]() 与
与![]() 之间的函数图像如图所示,下列说法:①小林与小军的速度之比为
之间的函数图像如图所示,下列说法:①小林与小军的速度之比为![]() ;②
;②![]() 时,小林到达
时,小林到达![]() 地;③
地;③![]() 时,小林与小军同时到达C地;④
时,小林与小军同时到达C地;④![]() 两地相距
两地相距![]() 千米,其中正确的有_________(只填序号)
千米,其中正确的有_________(只填序号)
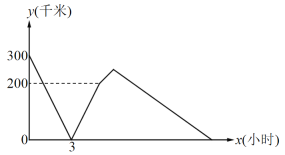
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县特色早餐种类繁多,色香味美,著名的种类有“干挑面”、“锅贴”、“青团子” “粢米饭”等.一数学兴趣小组在全校范围内随机抽取了一些同学进行“我最喜爱的特色早餐”调查活动,每位同学选择一种自己最喜欢的早餐种类,将调查结果绘制成如下两幅不完整的统计图.请根据图中的信息,解答下列问题:

(1)请将条形统计图补充完整.
(2)在扇形统计图中,表示“粢米饭”对应的扇形的圆心角是多少度?
(3)该校共有1200名学生,请你估计该校学生中最喜爱“青团子”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中国传统文化,某校组织了一次全体学生“汉字听写”大赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果作为样本进行整理,绘制成如下的统计图表:
组别 | 正确字数x | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |

根据以上信息完成下列问题:
(1)统计表中的![]() ________,
________,![]() ________,并补全条形统计图;扇形统计图中“C组“所对应的圆心角的度数是________;
________,并补全条形统计图;扇形统计图中“C组“所对应的圆心角的度数是________;
(2)已知该校共有600名学生,如果听写正确的字的个数不少于24个定为合格,请你估计该校本次听写比赛合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼。小丽在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,根据图中提供的信息,解答下列各题:
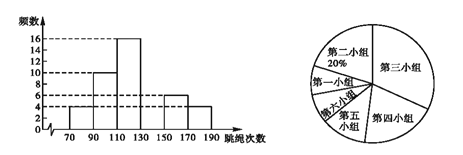
(1)本次调查共抽取了多少名学生?
(2)补全频数分布直方图;
(3)若全校共有1200名学生,跳绳成绩为优秀的约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com