
【题目】如图,AD为∠EAC的角平分线,DE⊥AE,DF⊥AC,∠EBD=∠FCD.

(1)判断△BDC的形状并说明理由;
(2)求证:CF-AF=AB.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)由角平分线上的点到两边的距离相等可知DE=DF,又由题意知∠DEB=∠DFC=90°,∠EBD=∠FCD可证三角形DEB≌三角形DFC,可得BD=CD,即可知△BDC的形状;
(2)由题意可得三角形ADE≌三角形ADF,可得AF=AE,由(1)知BE=CF,则可知CF-AF=AB.
解:(1)∵AD为∠EAC的平分线,DE⊥BE,DF⊥AC,
∴DE=DF,
∵∠DEB=∠DFC=90°,∠EBD=∠FCD,
∴三角形DEB≌三角形DFC,
∴BD=CD,
∴三角形BDC为等腰三角形;
(2)由题意可得∠DAE=∠DAF,AD=AD,∠AED=∠AFD,
则三角形ADE≌三角形ADF,可得AF=AE,
由(1)知BE=CF,CF-AF=BE-AE=AB.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AC是一棵大树,BF是一个斜坡,坡角为30°,某时刻太阳光垂直照射斜坡BF,树顶端A的影子落到斜坡上的点D处,已知BC=6m,BD=4m,求树AC的高度.(结果精确到0.1m.参考数据: ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p= ,且其日销售量y(kg)与时间t(天)的关系如表:
,且其日销售量y(kg)与时间t(天)的关系如表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() .
.![]() 绕着边
绕着边![]() 的中点
的中点![]() 旋转,
旋转,![]() ,
,![]() 分别交线段
分别交线段![]() 于点
于点![]() .
.

(1)观察:①如图2、图3,当![]() 或
或![]() 时,
时,![]() ________
________![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
②如图4,当![]() 时,
时,![]() ________
________![]() (填“
(填“![]() ”或“
”或“![]() ”)
”)
(2)猜想:如图1,当![]() 时,
时,![]() ________
________![]() ,证明你所得到的结论.
,证明你所得到的结论.
(3)如果![]() ,请求出
,请求出![]() 的度数和
的度数和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
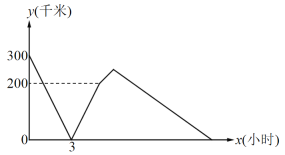
【题目】一条笔直的公路上顺次有![]() 三地,小军早晨
三地,小军早晨![]() 从
从![]() 地出发沿这条公路骑自行车前往
地出发沿这条公路骑自行车前往![]() 地,同时小林从
地,同时小林从![]() 地出发沿这条公路骑摩托车前往
地出发沿这条公路骑摩托车前往![]() 地,小林到地后休息了
地,小林到地后休息了 ![]() 个小时, 然后掉头原路原速返回追赶小军,经过一段时间后两人同时到达
个小时, 然后掉头原路原速返回追赶小军,经过一段时间后两人同时到达![]() 地,设两人行驶的时间为
地,设两人行驶的时间为![]() (小时),两人之间的距离为
(小时),两人之间的距离为![]() (千米),
(千米), ![]() 与
与![]() 之间的函数图像如图所示,下列说法:①小林与小军的速度之比为
之间的函数图像如图所示,下列说法:①小林与小军的速度之比为![]() ;②
;②![]() 时,小林到达
时,小林到达![]() 地;③
地;③![]() 时,小林与小军同时到达C地;④
时,小林与小军同时到达C地;④![]() 两地相距
两地相距![]() 千米,其中正确的有_________(只填序号)
千米,其中正确的有_________(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.

(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com