Question

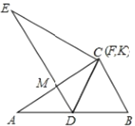
【题目】如图1，，，.绕着边的中点旋转，，分别交线段于点.

（1）观察：①如图2、图3，当或时，________（填“”，“”或“”）

②如图4，当时，________（填“”或“”）

（2）猜想：如图1，当时，________，证明你所得到的结论.

（3）如果，请求出的度数和的值.

Answer 1

【答案】（1）①= ②＞ （2）>，见解析 （3）15°；

【解析】

（1）①根据直角三角形斜边中线的性质可得CD=AD=BD=AB，分或时两种情况，可得AM=0或CK=0，即可得出；

②由∠BDC=60°可知∠ADC=120°，根据∠CDF=30°可求出∠ADM=30°，可得AM=DM，CK=KD，根据三角形的三边关系即可得答案；

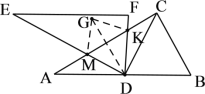
（2）如图，作点C关于FD的对称点G，连接GK，GM，GD．根据直角三角形斜边中线的性质及等腰三角形的性质可证明，利用SAS可证明△ADM≌△GDM，根据全等三角形的性质可得GM=AM，根据三角形三边关系即可得答案；

（3）根据勾股定理的逆定理求得∠GKM=90°，由轴对称的性质可得∠CKG=90°，∠FKC=∠CKG=45°，根据三角形的外角定理，可得∠CDF=15°；在Rt△GKM中，∠MGK=∠DGK+∠MGD=∠A+∠ACD=60°，可得∠GMK=30°，利用余弦的定义可得=cos30°，即可得答案．

（1）①∵在中，是的中点，∠ACB=90°，∠A=30°，

∴，，

∴，

如图，当时，，点A与点M重合，

∵AD=CD，

∴CK=MK，

∵AM=0，

∴AM+CK=MK，

如图，当∠CDF=0°时，

∵△ABC≌△EDF，

∴DF=BC，∠EDF=∠B=60°，

∴DF=CD，即点C与点F、K重合，

∵∠ACD=30°，∠EDF=60°，

∴∠CDM=90°，

∴AM=MK，

∵CK=0，

∴

综上所述：，

故答案为：=

②由①，得，，

∴∠ADC=120°，

∵，，，

∴，

∴，

∴

∴在中（两边之和大于第三边）.

（2）作点关于的对称点，连接，，，则，，

∵是的中点，

∴，

∴，，

∴，

∵，

∴，

∴，

在△ADM和△GDM中，，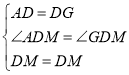

∴，

∴，

∵，

∴

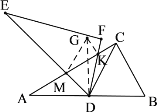
（3）如图，由（2），得，

∵，

∴，

∴，

∵点关于的对称点为，

∴，，

由（1）可知：，

∵，

∴，

在中，，

∴，

∴GK=MG，

∴MK==GM，

∴，

∴，

综上可得：的度数为，的值为．