
【题目】如图,![]() 为
为![]() 内一点,过点
内一点,过点![]() 分别作
分别作![]() ,
,![]() 的平行线,交
的平行线,交![]() 的四边于
的四边于![]() 、
、![]() 、
、![]() 、
、![]() 四点,若
四点,若![]() 面积为6,
面积为6,![]() 面积为4,则
面积为4,则![]() 的面积为( )
的面积为( )

A.![]() B.
B.![]() C.1D.2
C.1D.2
【答案】C
【解析】
根据平行四边形的性质得到四个平行四边形,且S△AEP=S△AGP,S△PHC=S△PFC,S△ABC= S△ADC,
利用面积比较的关系即可求出答案.
由题意知:四边形BHPE、四边形AEPG、四边形HCFP、四边形GPFD均为平行四边形,
∴S△AEP=S△AGP,S△PHC=S△PFC,S△ABC= S△ADC,
又S△ABC=S△AEP+S四边形BHPE+S△PHC-S△APC①,
S△ADC=S△AGP+S四边形GPFD+S△PFC+S△APC②,
②-①得,0=S四边形BHPE-S四边形GPFD+2S△APC,
即2S△APC=6-4=2,
S△APC=1.
故选:C.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中,已知,
中,已知,![]() ,
,![]() 于D,
于D,![]() ,
,![]() ,如何求AD的长呢?
,如何求AD的长呢?
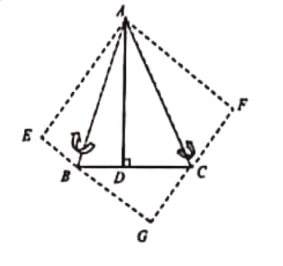
心怡同学灵活运用对称知识,将图形进行翻折变换,巧妙地解答了此题,
请按照她的思路,探究并解答下列问题:
(1)分别以AB、AC为对称轴,画出![]() 、
、![]() 的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
(2)设![]() ,利用勾股定理,建立关于x的方程模型,求出x的值.
,利用勾股定理,建立关于x的方程模型,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,已知直线
为原点,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,如图①.
轴对称,如图①.
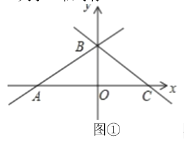
(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,直线
的坐标为________,直线![]() 的解析式为________.
的解析式为________.
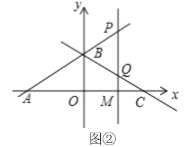
(2)点![]() 是
是![]() 轴上的一个动点(点
轴上的一个动点(点![]() 不与点
不与点![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() .交直线
.交直线![]() 于点
于点![]() (图②).
(图②).
①如图②,当点![]() 在
在![]() 轴的正半轴上时,若
轴的正半轴上时,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标;
的坐标;
②连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠ABC=60°,BC=8,点 D 是 BC 边的中点,点 E 是边 AC上一点,过点 D 作 ED 的垂线交边 AC 于点 F,若 AC=7CF,且 DE 恰好平分△ABC 的周长,则△ABC 的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的道路AB上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,假设他们分别以不同的速度匀速行驶,甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的函数图象如图.
(1)A地与B地相距______km,甲的速度为______km/分;
(2)求甲、乙两人相遇时,乙行驶的路程;
(3)当乙到达终点A时,甲还需多少分钟到达终点B?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com