
【题目】如图,![]() 中,已知,
中,已知,![]() ,
,![]() 于D,
于D,![]() ,
,![]() ,如何求AD的长呢?
,如何求AD的长呢?
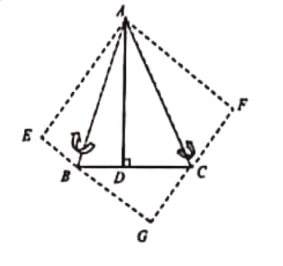
心怡同学灵活运用对称知识,将图形进行翻折变换,巧妙地解答了此题,
请按照她的思路,探究并解答下列问题:
(1)分别以AB、AC为对称轴,画出![]() 、
、![]() 的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
(2)设![]() ,利用勾股定理,建立关于x的方程模型,求出x的值.
,利用勾股定理,建立关于x的方程模型,求出x的值.
【答案】(1)见详解;(2)18
【解析】
(1)先根据△ABD≌△ABE,△ACD≌△ACF,得出∠EAF=90°;再根据对称的性质得到AE=AF,从而说明四边形AEGF是正方形;
(2)利用勾股定理,建立关于x的方程模型(x-6)2+(x-9)2=152,求出AD=x=6.
解:(1)证明:由题意可得:△ABD≌△ABE,△ACD≌△ACF
∴∠DAB=∠EAB,∠DAC=∠FAC,又∠BAC=45°
∴∠EAF=90°
又∵AD⊥BC
∴∠E=∠ADB=90°,∠F=∠ADC=90°
又∵AE=AD,AF=AD
∴AE=AF
∴四边形AEGF是正方形
(2)解:设AD=x,则AE=EG=GF=x
∵BD=6,DC=9
∴BE=6,CF=9
∴BG=x-6,CG=x-9
在Rt△BGC中,BG2+CG2=BC2
∴(x-6)2+(x-9)2=152
∴(x-6)2+(x-9)2=152,化简得,x2-15x-54=0,整理得(x-18)(x+3)=0
解得x1=18,x2=-3(舍去)
所以AD=x=18


科目:初中数学 来源: 题型:
【题目】甲、乙两家体育用品商店出售同样的乒乓球和乒乓拍,乒乓球拍每幅定价20元,乒乓球每盒定价5元,现两家商店搞促销活动.甲店:每买一副球拍送一盒乒乓球;乙店:按定价的8折优惠.某班级需购球拍4副,乒乓球若干盒(不少于4盒).
(1)设购买乒乓球盒数为![]() (盒),在甲店购买的付款数为
(盒),在甲店购买的付款数为![]() (元);在乙店购买的付款数为
(元);在乙店购买的付款数为![]() (元),分别写出
(元),分别写出![]() 和
和![]() 与
与![]() 的函数关系式,并写出定义域.
的函数关系式,并写出定义域.
(2)就乒乓球的盒数讨论去哪家购买合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)

查看答案和解析>>
科目:初中数学 来源: 题型:
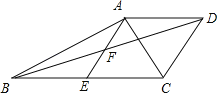
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
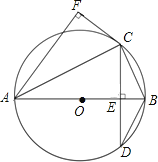
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
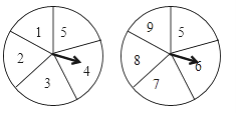
【题目】如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何学的产生,源于人们对土地面积测量的需要,以面积早就成为人们认识图形性质与几何证明的有效工具,可以说几何学从一开始便与面积结下了不解之缘.我们已经掌握了平行四边形面积的求法,但是一般四边形的面积往往不易求得,那么我们能否将其转化为平行四边形来求呢?
(1)方法1:如图①,连接四边形![]() 的对角线
的对角线![]() ,
,![]() ,分别过四边形
,分别过四边形![]() 的四个顶点作对角线的平行线,所作四条线相交形成四边形
的四个顶点作对角线的平行线,所作四条线相交形成四边形![]() ,易证四边形
,易证四边形![]() 是平行四边形.请直接写出S四边形ABCD和
是平行四边形.请直接写出S四边形ABCD和![]() 之间的关系:_______________.
之间的关系:_______________.
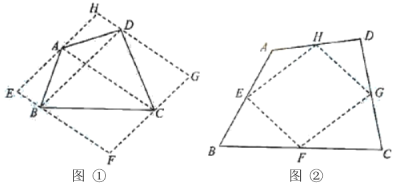
方法2:如图②,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)请直接写出S四边形ABCD与![]() 之间的关系:_____________.
之间的关系:_____________.
方法3:如图③,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .先将四边形
.先将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;再将四边形
在同一直线上;再将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;最后将四边形
在同一直线上;最后将四边形![]() 沿
沿![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,得到四边形
重合,得到四边形![]() ;
;
(4)由旋转、平移可得![]() _________,
_________,![]() _________,所以
_________,所以![]() ,所以点
,所以点![]() ,
,![]() ,
,![]() 在同一直线上,同理,点
在同一直线上,同理,点![]() ,
,![]() ,
,![]() 也在同一点线上,所以我们拼接成的图形是一个四边形.
也在同一点线上,所以我们拼接成的图形是一个四边形.
(5)求证:四边形![]() 是平行四边形.
是平行四边形.

(注意:请考生在下面2题中任选一题作答如果多做,则按所做的第一题计分)
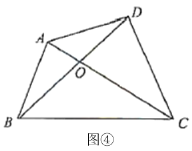
(6)应用1:如图④,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=
,则S四边形ABCD= ![]() .
.
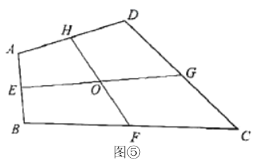
(7)应用2:如图⑤,在四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=___________
,则S四边形ABCD=___________![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com