
【题目】几何学的产生,源于人们对土地面积测量的需要,以面积早就成为人们认识图形性质与几何证明的有效工具,可以说几何学从一开始便与面积结下了不解之缘.我们已经掌握了平行四边形面积的求法,但是一般四边形的面积往往不易求得,那么我们能否将其转化为平行四边形来求呢?
(1)方法1:如图①,连接四边形![]() 的对角线
的对角线![]() ,
,![]() ,分别过四边形
,分别过四边形![]() 的四个顶点作对角线的平行线,所作四条线相交形成四边形
的四个顶点作对角线的平行线,所作四条线相交形成四边形![]() ,易证四边形
,易证四边形![]() 是平行四边形.请直接写出S四边形ABCD和
是平行四边形.请直接写出S四边形ABCD和![]() 之间的关系:_______________.
之间的关系:_______________.
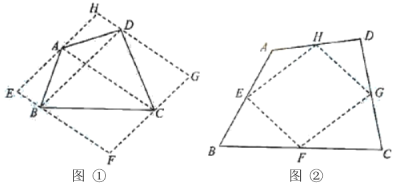
方法2:如图②,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)请直接写出S四边形ABCD与![]() 之间的关系:_____________.
之间的关系:_____________.
方法3:如图③,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .先将四边形
.先将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;再将四边形
在同一直线上;再将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;最后将四边形
在同一直线上;最后将四边形![]() 沿
沿![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,得到四边形
重合,得到四边形![]() ;
;
(4)由旋转、平移可得![]() _________,
_________,![]() _________,所以
_________,所以![]() ,所以点
,所以点![]() ,
,![]() ,
,![]() 在同一直线上,同理,点
在同一直线上,同理,点![]() ,
,![]() ,
,![]() 也在同一点线上,所以我们拼接成的图形是一个四边形.
也在同一点线上,所以我们拼接成的图形是一个四边形.
(5)求证:四边形![]() 是平行四边形.
是平行四边形.

(注意:请考生在下面2题中任选一题作答如果多做,则按所做的第一题计分)
(6)应用1:如图④,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=
,则S四边形ABCD= ![]() .
.
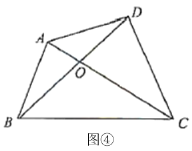
(7)应用2:如图⑤,在四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=___________
,则S四边形ABCD=___________![]()
【答案】(1)S四边形ABCD![]() ;(2)见详解;(3)S四边形ABCD
;(2)见详解;(3)S四边形ABCD ![]() ;(4)AEO,OEB;(5)见详解;(6)
;(4)AEO,OEB;(5)见详解;(6)![]() ;(7)
;(7)![]()
【解析】
(1)先证四边形AEBO, 四边形BFCO, 四边形CGDO, 四边形DHAO都是平行四边形,可得S△ABO=![]() S四边形AEBO, S△BCO=
S四边形AEBO, S△BCO=![]() S四边形BFCO, S△CDO=
S四边形BFCO, S△CDO=![]() S四边形CGDO, SADO=
S四边形CGDO, SADO=![]() S四边形DHAO,
S四边形DHAO,
即可得出结论;
(2)证明![]() ,
,![]() 和
和![]() ,
,![]() ,即可得出结论;
,即可得出结论;
(3)由![]() ,
,![]() 可得S四边形MNHE=
可得S四边形MNHE=![]() S△ABD, S四边形MNGF=
S△ABD, S四边形MNGF=![]() S△CBD,即可得出结论;
S△CBD,即可得出结论;
(4)有旋转的定义即可得出结论;
(5)先证![]() ,得到
,得到![]() ,再证
,再证![]() ,即可得出结论;
,即可得出结论;
(6)应用方法1,过点H作HM⊥EF与点M,再计算即可得出答案;
(7)应用方法3,过点O作OM⊥IK与点M, 再计算即可得出答案.
解:方法一:如图,

∵EF∥AC∥HD,EH∥DB∥FG,
∴四边形AEBO, 四边形BFCO, 四边形CGDO, 四边形DHAO都是平行四边形,
∴S△ABO=![]() S四边形AEBO, S△BCO=
S四边形AEBO, S△BCO=![]() S四边形BFCO, S△CDO=
S四边形BFCO, S△CDO=![]() S四边形CGDO, SADO=
S四边形CGDO, SADO=![]() S四边形DHAO,
S四边形DHAO,
∴![]() .
.
故答案为![]() .
.
方法二:如图,连接![]() .
.

(1)![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点
中点
![]() .
.![]() .
.
![]()
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点
中点
![]() .
.![]()
![]() ,
,![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
(2)![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点
中点
![]() .
.![]() .
.
∴S四边形MNHE=![]() S△ABD, S四边形MNGF=
S△ABD, S四边形MNGF=![]() S△CBD,
S△CBD,
∴![]()
故答案为![]() .
.
方法3.(1)有旋转可知![]() ;
;![]() .
.
故答案为∠AEO;∠OEB.
(2)证明:有旋转知.

![]() .
.![]()
![]()
![]()
![]() 旋转.
旋转.
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
应用1:如图,应用方法1,过点H作HM⊥EF与点M,

∵![]() ,
,
∴∠AEM=60°, ∠EHM=30°,
∵![]() ,
,![]() ,
,
∴EM=3,EH=6,EF=8,
∴HM=![]() =
=![]() ,
,
∴![]() =EF·HM=24
=EF·HM=24![]()
∴![]() =
=![]() ,
,
故答案为![]() .
.
应用2:如图,应用方法3,过点O作OM⊥IK与点M,
 ,
,
∵![]() ,
,
∴∠MIO=60°, ∠IOM=30°,
∵![]() ,
,![]() ,
,
∴IM=3,OI=6,IK=8,
∴OM=![]() =
=![]() ,
,
∴![]() =KI·OM=24
=KI·OM=24![]()
∴S四边形ABCD=![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,为美化校园环境,某校计划在一块长为100米,宽为60米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为![]() 米.
米.
(1)如果通道所占面积是整个长方形空地面积的![]() ,求出此时通道的宽;
,求出此时通道的宽;
(2)如果通道宽![]() (米)的值能使关于
(米)的值能使关于![]() 的方程
的方程![]() 有两个相等的实数根,并要求修建的通道的宽度不少于5米且不超过12米,求出此时通道的宽.
有两个相等的实数根,并要求修建的通道的宽度不少于5米且不超过12米,求出此时通道的宽.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单 位:s)(0<t<![]() )。
)。
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,已知,
中,已知,![]() ,
,![]() 于D,
于D,![]() ,
,![]() ,如何求AD的长呢?
,如何求AD的长呢?
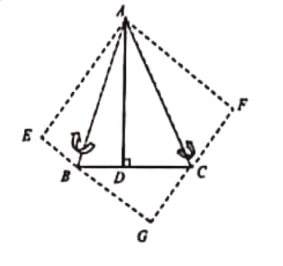
心怡同学灵活运用对称知识,将图形进行翻折变换,巧妙地解答了此题,
请按照她的思路,探究并解答下列问题:
(1)分别以AB、AC为对称轴,画出![]() 、
、![]() 的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
(2)设![]() ,利用勾股定理,建立关于x的方程模型,求出x的值.
,利用勾股定理,建立关于x的方程模型,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,已知直线
为原点,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,如图①.
轴对称,如图①.
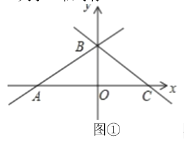
(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,直线
的坐标为________,直线![]() 的解析式为________.
的解析式为________.
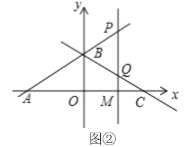
(2)点![]() 是
是![]() 轴上的一个动点(点
轴上的一个动点(点![]() 不与点
不与点![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() .交直线
.交直线![]() 于点
于点![]() (图②).
(图②).
①如图②,当点![]() 在
在![]() 轴的正半轴上时,若
轴的正半轴上时,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标;
的坐标;
②连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com