
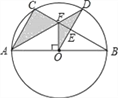
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2![]() .
.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
【答案】(1)6;(2)![]() .
.
【解析】试题(1)由∠BOF=90°,∠B=30°,得出FO=![]() , OB=6,AB=2OB=12,由AB为⊙O的直径,得到∠ACB=90°,故AC=
, OB=6,AB=2OB=12,由AB为⊙O的直径,得到∠ACB=90°,故AC=![]() AB=6;
AB=6;
(2)先证Rt△ACF≌Rt△AOF,得出阴影部分的面积=△AOD的面积,求出三角形的面积即可.
试题解析:(1)∵OF⊥AB,∴∠BOF=90°,∵∠B=30°,FO=![]() ,∴OB=6,AB=2OB=12,又∵AB为⊙O的直径,∴∠ACB=90°,∴AC=
,∴OB=6,AB=2OB=12,又∵AB为⊙O的直径,∴∠ACB=90°,∴AC=![]() AB=6;
AB=6;
(2)∵由(1)可知,AB=12,∴AO=6,即AC=AO,在Rt△ACF和Rt△AOF中,∵AF=AF,AC=AO,∴Rt△ACF≌Rt△AOF,∴∠FAO=∠FAC=30°,∴∠DOB=60°,过点D作DG⊥AB于点G,∵OD=6,∴DG=![]() ,∴
,∴![]() ,即
,即![]() .
.


科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
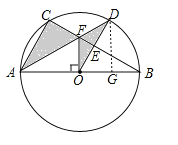
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若圆的一条弦把圆分成度数比为1:4的两段弧,则弦所对的圆周角等于( )
A. 36° B. 72° C. 36°或144° D. 72°或108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机可以通过“个人热点”功能实现移动网络共享,小明和小亮准备到操场上测试个人热点连接的有效距离,他们从相距![]() 的
的![]() ,
,![]() 两地相向而行.图中
两地相向而行.图中![]() ,
,![]() 分别表示小明、小亮两人离
分别表示小明、小亮两人离![]() 地的距离
地的距离![]() 与步行时间
与步行时间![]() 之间的函数关系,其中
之间的函数关系,其中![]() 的关系式为
的关系式为![]() .根据图象回答下列问题:
.根据图象回答下列问题:

(1)请写出![]() 的关系式___________;
的关系式___________;
(2)小明和小亮出发后经过了多长时间相遇?
(3)如果手机个人热点连接的有效距离不超过![]() ,那么他们出发多长时间才能连接成功?连接持续了多长时间?
,那么他们出发多长时间才能连接成功?连接持续了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数
在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数![]() 与
与![]() 的图象上,对角线
的图象上,对角线![]() 于点
于点![]() ,
,![]() 轴于点
轴于点![]() .
.
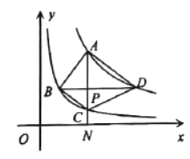
(1)若![]() ,试求
,试求![]() 的值;
的值;
(2)当![]() ,点
,点![]() 是线段
是线段![]() 的中点时,试判断四边形
的中点时,试判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
(3)直线![]() 与
与![]() 轴相交于
轴相交于![]() 点.当四边形
点.当四边形![]() 为正方形时,请求出
为正方形时,请求出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 A、B 两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为 1,E 是⊙C 上的一动点,则△ABE 面积的最大值为( )
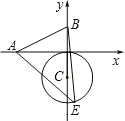
A. ![]() B. 3+
B. 3+![]() C. 3+
C. 3+![]() D. 4+
D. 4+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com