
【题目】在平面直角坐标系xoy中,直线![]() (k为常数)与抛物线
(k为常数)与抛物线![]() 交于A,B两点,且A点在
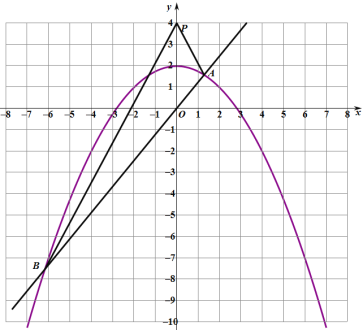
交于A,B两点,且A点在![]() 轴右侧,P点的坐标为(0,4)连接PA,PB.(1)△PAB的面积的最小值为____;(2)当
轴右侧,P点的坐标为(0,4)连接PA,PB.(1)△PAB的面积的最小值为____;(2)当![]() 时,
时,![]() =_______
=_______
【答案】![]() 16
16
【解析】
(1)设A(m,km),B(n,kn),联立解析式,利用根与系数的关系建立![]() 之间的关系,列出面积函数关系式,利用二次函数的性质求解最小值即可;
之间的关系,列出面积函数关系式,利用二次函数的性质求解最小值即可;
(2)先证明![]() 平分
平分![]() 得到
得到![]() ,把
,把![]() 转化为
转化为![]() ,利用两点间的距离公式再次转化,从而可得答案.
,利用两点间的距离公式再次转化,从而可得答案.
解:(1)如图,设A(m,km),B(n,kn),其中m![]() 0,n
0,n![]() 0.
0.
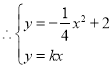
得: ![]() 即
即![]() ,
,
∴![]()
![]()
![]()
∴当k=0时,△PAB面积有最小值,最小值为![]()
故答案为![]() .
.
(2)设设A(m,km),B(n,kn),其中m![]() 0,n
0,n![]() 0.
0.
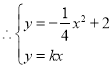
得: ![]() 即
即![]() ,
,
∴![]()
设直线PA的解析式为y=ax+b,将P(0,4),A(m,km)代入得:
![]() ,解得:
,解得: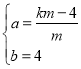 ,
,
∴![]()
令y=0,得![]()
∴直线PA与x轴的交点坐标为![]() .
.
同理可得,直线PB的解析式为![]()
直线PB与x轴交点坐标为![]() .
.
∵ 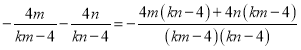

∴直线PA、PB与x轴的交点关于y轴对称,即直线PA、PB关于y轴对称.
![]() 平分
平分![]() ,
,
![]()
![]() 到
到![]() 的距离相等,
的距离相等,
![]()
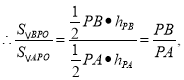
而 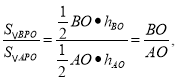
∴![]() ,
,
过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,
,
则![]()
![]()
∴![]()
∴![]()
![]()
![]()
![]()
∵![]() ∴
∴![]()
∴![]()
∴![]()

故答案为:![]()


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
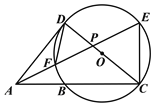
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由西向东航行,在A处测得北偏东60°方向上有一座灯塔C,再向东续航行60km到达B处,这时测得灯塔C在北偏东30°方向上,已知在灯塔C的周围47km内有暗礁,问这艘船继续向东航行是否安全?
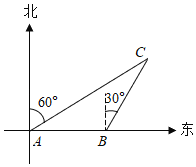
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 过点A(1,0),B(3,0)两点,与y轴交于点C,
过点A(1,0),B(3,0)两点,与y轴交于点C,![]() .
.
(1)求抛物线的解析式;
(2)点![]() 为抛物线在直线
为抛物线在直线![]() 下方图形上的一动点,当
下方图形上的一动点,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为线段
为线段![]() 上的一动点,问:
上的一动点,问:![]() 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由
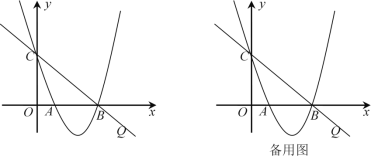
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是![]() 上一点,∠ADC=∠G.
上一点,∠ADC=∠G.
(1)求证:∠1=∠2;
(2)点C关于DG的对称点为F,连结CF,当点F落在直径AB上时,CF=10,tan∠1=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识改变世界,科技改变生活。导航设备的不断更新方便了人们的出行。如图,某校组织学生乘车到蒲江茶叶基地C地进行研学活动,车到达A地后,发现C地恰好在A地的正东方向,且距A地9.1千米,导航显示车辆应沿南偏东60°方向行驶至B地,再沿北偏东53°方向行驶一段距离才能到达C地,求B、C两地的距离(精确到个位)
(参考数据![]() )
)
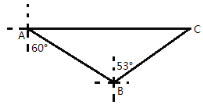
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
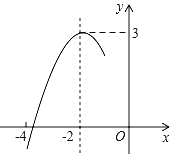
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地高速铁路建设成功,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,下列说法:
①甲、乙两地相距1800千米;
②点B的实际意义是两车出发后4小时相遇;
③m=6,n=900;
④动车的速度是450千米/小时.
其中不正确的是( )
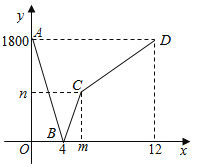
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
(1)求抛物线的解析式;
(2)![]() 为抛物线上的一个动点,点
为抛物线上的一个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() .当点
.当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
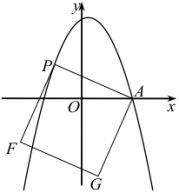
(3)![]()
![]() 是抛物线上一动点,连接
是抛物线上一动点,连接![]() ,以
,以![]() 为边作图示一侧的正方形
为边作图示一侧的正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小与位置也随之改变,当顶点
的运动,正方形的大小与位置也随之改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,求对应的
轴上时,求对应的![]() 点坐标.
点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com