
【题目】抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
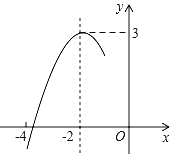
A.1个B.2个C.3个D.4个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )
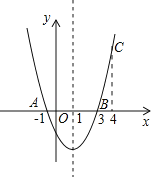
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
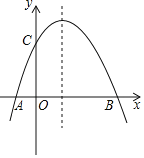
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
(3)点![]() 为
为![]() 轴上一动点,在抛物线上是否存在一点
轴上一动点,在抛物线上是否存在一点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 四点构成的四边形为平行四边形?若存在,求点
四点构成的四边形为平行四边形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线![]() (k为常数)与抛物线
(k为常数)与抛物线![]() 交于A,B两点,且A点在
交于A,B两点,且A点在![]() 轴右侧,P点的坐标为(0,4)连接PA,PB.(1)△PAB的面积的最小值为____;(2)当
轴右侧,P点的坐标为(0,4)连接PA,PB.(1)△PAB的面积的最小值为____;(2)当![]() 时,
时,![]() =_______
=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
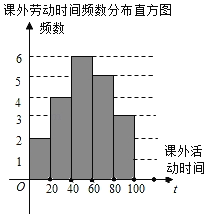
【题目】遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:h)的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.
课外劳动时间频数分布表
劳动时间分组 | 频数 | 频率 |
0≤t<20 | 2 | 0.1 |
20≤t<40 | 4 | m |
40≤t<60 | 6 | 0.3 |
60≤t<80 | a | 0.25 |
80≤t<100 | 3 | 0.15 |
解答下列问题:
(1)频数分布表中a= ,m= ;将频数分布直方图补充完整;
(2)若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于60h的人数;
(3)已知课外劳动时间在60h≤t<80h的男生人数为2人,其余为女生,现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数y1=![]() ,y2=﹣
,y2=﹣![]() (k>0).
(k>0).
(1)当2≤x≤3时,函数y1的最大值是a,函数y2的最小值是a﹣4,求a和k的值.
(2)设m≠0,且m≠﹣1,当x=m时,y1=p;当x=m+1时,y1=q.圆圆说:“p一定大于q”.你认为圆圆的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
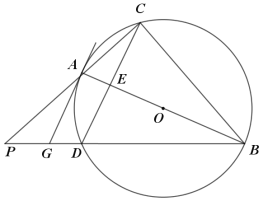
【题目】如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿直线AB折叠得到△ABD,交⊙O于点D.连接CD交AB于点E,延长BD和CA相交于点P,过点A作AG∥CD交BP于点G.
(1)求证:直线GA是⊙O的切线;
(2)求证:AC2=GDBD;
(3)若tan∠AGB=![]() ,PG=6,求cos∠P的值.
,PG=6,求cos∠P的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全球关注的抗击“新冠肺炎”中某跨国科研中心的一个团队研制了一种助治“新冠附炎”的新药,在试验药效时发现,如果成人按规定的制量服用,那么服药后2小时血液中含药量最高,达每毫升8微克(1微克=![]() 毫克),接着逐步安减,10小时时血液中含药最为每毫升3微克,每毫升血液中含药量
毫克),接着逐步安减,10小时时血液中含药最为每毫升3微克,每毫升血液中含药量![]() (微克)随时间
(微克)随时间![]() (小时)的变化如图所示.
(小时)的变化如图所示.
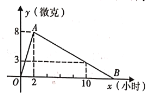
(1)分别求线段![]() 所表示的函数关系式;
所表示的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时对治病是有效的,那么这个有效时间是多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com