
【题目】如图,在![]() 中
中![]()
![]() ,连接
,连接![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() 的点(点
的点(点![]() 不与点
不与点![]() 重合),
重合),![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)求![]() ,
,![]() 的长;
的长;
(2)求证:![]() ~
~![]() ;
;
(3)当![]() 时,请直接写出
时,请直接写出![]() 的长.
的长.
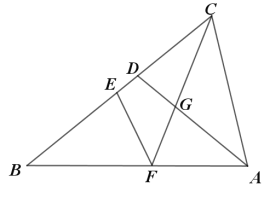
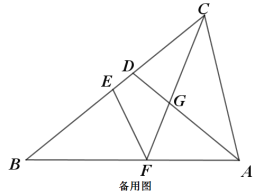
【答案】(1)AD=10,BD=10;(2)见解析;(3)AG=![]() .
.
【解析】
(1)由![]() 可证明△ABC∽△DAC,通过相似比即可求出AD,BD的长;
可证明△ABC∽△DAC,通过相似比即可求出AD,BD的长;
(2)由(1)可证明∠B=∠DAB,再根据已知条件证明∠AFC=∠BEF即可;
(3)过点C作CH∥AB,交AD的延长线于点H,根据平行线的性质得到![]() ,计算出CH和AH的值,由已知条件得到
,计算出CH和AH的值,由已知条件得到![]() ≌
≌![]() ,设AG=x,则AF=15-x,HG=18-x,再由平行线的性质得到
,设AG=x,则AF=15-x,HG=18-x,再由平行线的性质得到![]() ,表达出即可解出x,即AG的值.
,表达出即可解出x,即AG的值.
解:(1)∵![]() ,
,
∴![]() ,
,
又∵∠ACB=∠DCA,
∴△ABC∽△DAC,
∴![]() ,即
,即![]() ,
,
解得:CD=8,AD=10,
∴BD=BC-CD=18-8=10,
∴AD=10,BD=10;
(2)由(1)可知,AD=BD=10,
∴∠B=∠DAB,
∵∠AFE=∠B+∠BEF,
∴∠AFC+∠CFE=∠B+∠BEF,
∵![]() ,
,
∴∠AFC=∠BEF,
又∵∠B=∠DAB,
∴![]() ~
~![]() ;
;
(3)如图,过点C作CH∥AB,交AD的延长线于点H,
∴![]() ,
,
即![]() ,解得:CH=12,HD=8,
,解得:CH=12,HD=8,
∴AH=AD+HD=18,
若![]() ,
,
则![]() ≌
≌![]() ;
;
∴BF=AG,
设AG=x,则AF=15-x,HG=18-x,
∵CH∥AB,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() (舍去)
(舍去)
∴AG=![]() .
.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】解不等式组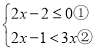
请结合题意填空,完成本题的解答
(1)解不等式①,得___________;
(2)解不等式②,得___________;
(3)把不等式①和②的解集在数轴上表示出来:

(4)原不等式组的解集为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:

(Ⅰ)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为______;
的值为______;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校一周的课外阅读时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C,D为⊙O上两点,且在直径AB两侧,连结CD交AB于点E,G是![]() 上一点,∠ADC=∠G.
上一点,∠ADC=∠G.
(1)求证:∠1=∠2;
(2)点C关于DG的对称点为F,连结CF,当点F落在直径AB上时,CF=10,tan∠1=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
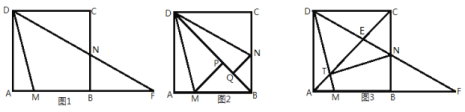
【题目】如图,在正方形ABCD中,点M、N分别在AB、BC边上,∠MDN=45°.
(1)如图1,DN交AB的延长线于点F. 求证:![]() ;
;
(2)如图2,过点M作MP⊥DB于P,过N作NQ⊥BD于![]() ,若
,若![]() ,求对角线BD的长;
,求对角线BD的长;
(3)如图3,若对角线AC交DM,DF分别于点T,E.判断△DTN的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
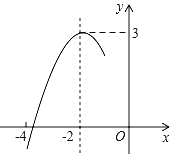
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A,C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD,AB于点M、N,作射线DF交射线CA于点G.
(1)求证:EF=DE;
(2)当AF=2时,求GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为4,分别取AC,BC两边的中点A1,B1,记△A1B1C的面积为S1;再分别取A1C,B1C的中点A2,B2,记△A2B2C的面积为S2,再分别取A2C,B2C的中点A3,B3,记△A3B3C的面积为S3;则S3的值等于_____.
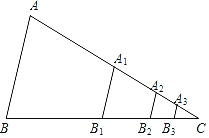
查看答案和解析>>
科目:初中数学 来源: 题型:
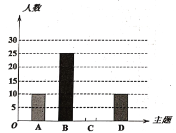
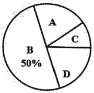
【题目】某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“A”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com