
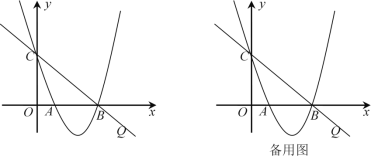
【题目】已知抛物线![]() 过点A(1,0),B(3,0)两点,与y轴交于点C,
过点A(1,0),B(3,0)两点,与y轴交于点C,![]() .
.
(1)求抛物线的解析式;
(2)点![]() 为抛物线在直线
为抛物线在直线![]() 下方图形上的一动点,当
下方图形上的一动点,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为线段
为线段![]() 上的一动点,问:
上的一动点,问:![]() 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由
【答案】(1)![]() .(2)(
.(2)(![]() ,
,![]() ).(3)存在,
).(3)存在,![]() .
.
【解析】
(1)设抛物线的解析式为![]() ,求出点C坐标,结合点A和点B坐标,利用待定系数法求解即可;
,求出点C坐标,结合点A和点B坐标,利用待定系数法求解即可;
(2)设直线BC的解析式为:![]() ,求出BC的解析式,过点P作y轴的平行线交BC于点H,设出点P的坐标,利用
,求出BC的解析式,过点P作y轴的平行线交BC于点H,设出点P的坐标,利用![]() 求出表达式,从而得到取最大值时点P的坐标;
求出表达式,从而得到取最大值时点P的坐标;
(3)过点C作与y轴夹角为![]() 的直线CH,过点A作
的直线CH,过点A作![]() 于H,得到
于H,得到![]() ,得到
,得到![]() 时值最小,分别求出HC和AH的表达式,联立求出x,从而得到点H坐标,再结合点A坐标求出AH的长,即可得到结果.
时值最小,分别求出HC和AH的表达式,联立求出x,从而得到点H坐标,再结合点A坐标求出AH的长,即可得到结果.
解:(1)抛物线![]() 过点A(1,0),B(3,0)两点,
过点A(1,0),B(3,0)两点,![]() ,
,
∵点C的坐标为(0,3),
设抛物线的解析式为![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)设直线BC的解析式为:![]() ,
,
则![]() ,
,
解得:![]() ,
,
故直线BC的解析式为:![]() ,
,
过点P作y轴的平行线交BC于点H
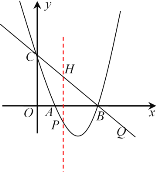
设点P的坐标为(x,![]() ),则点H的坐标为(x,
),则点H的坐标为(x,![]() )
)
则![]()
∵![]()
∴![]() 面积有最大值,此时
面积有最大值,此时![]()
故点P的坐标为(![]() ,
,![]() );
);
(3)存在,理由如下
如图,过点C作与y轴夹角为![]() 的直线CH,过点A作
的直线CH,过点A作![]() 于H
于H
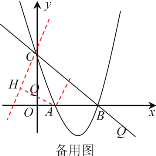
则![]() ,
,
∴![]() 时值最小
时值最小
直线HC所在表达式中的k的值为![]() ,直线HC的表达式为:
,直线HC的表达式为:![]() ①
①
则直线AH所在表达式中的k的值为:![]()
则直线AH所在表达式为:![]() ,将点A的坐标代入上式并解得:
,将点A的坐标代入上式并解得:
则直线AH所在表达式为:![]() ②
②
联立①②并解得:![]()
故点H(![]() ,
,![]() ),而点A(1,0)
),而点A(1,0)
则![]()
即:![]() 的最小值为
的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )

A.△DEF是等边三角形
B.△ADF≌△BED≌△CFE
C.DE=![]() AB
AB
D.S△ABC=3S△DEF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业承接了27000件产品的生产任务,计划安排甲、乙两个车间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
(1)求甲、乙两个车间各有多少名工人参与生产?
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变.
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
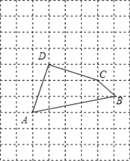
【题目】如图,将四边形ABCD放在每个小正方形的边长为1的网格中,点A.B、C、D均落在格点上.
(Ⅰ)计算AD2+DC2+CB2的值等于_____;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AD2+DC2+CB2,并简要说明画图方法(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
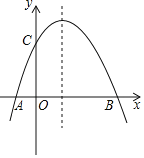
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
(3)点![]() 为
为![]() 轴上一动点,在抛物线上是否存在一点
轴上一动点,在抛物线上是否存在一点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 四点构成的四边形为平行四边形?若存在,求点
四点构成的四边形为平行四边形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
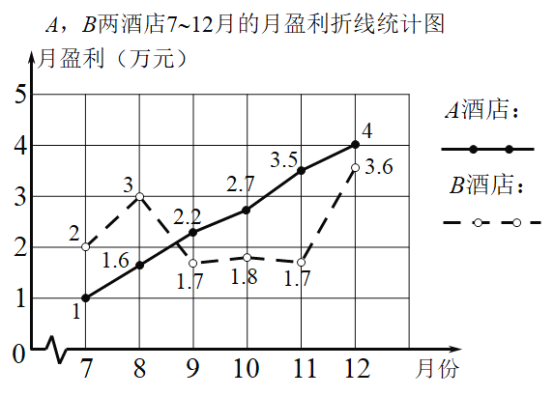
【题目】A,B两家酒店规模相当,去年下半年的月盈利折线统计图如图所示.
(1)要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量;
(2)已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元).根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线![]() (k为常数)与抛物线
(k为常数)与抛物线![]() 交于A,B两点,且A点在
交于A,B两点,且A点在![]() 轴右侧,P点的坐标为(0,4)连接PA,PB.(1)△PAB的面积的最小值为____;(2)当
轴右侧,P点的坐标为(0,4)连接PA,PB.(1)△PAB的面积的最小值为____;(2)当![]() 时,
时,![]() =_______
=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
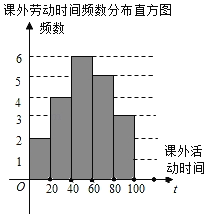
【题目】遵义市各校都在深入开展劳动教育,某校为了解七年级学生一学期参加课外劳动时间(单位:h)的情况,从该校七年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数分布直方图.
课外劳动时间频数分布表
劳动时间分组 | 频数 | 频率 |
0≤t<20 | 2 | 0.1 |
20≤t<40 | 4 | m |
40≤t<60 | 6 | 0.3 |
60≤t<80 | a | 0.25 |
80≤t<100 | 3 | 0.15 |
解答下列问题:
(1)频数分布表中a= ,m= ;将频数分布直方图补充完整;
(2)若七年级共有学生400人,试估计该校七年级学生一学期课外劳动时间不少于60h的人数;
(3)已知课外劳动时间在60h≤t<80h的男生人数为2人,其余为女生,现从该组中任选2人代表学校参加“全市中学生劳动体验”演讲比赛,请用树状图或列表法求所选学生为1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
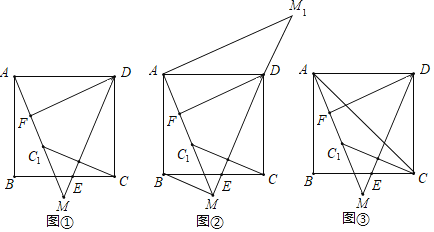
【题目】如图,在正方形ABCD中,点E是边BC上任意一点(点E不与点B、C重合),连结DE,点C关于DE的对称点为C1,连结AC1并延长交DE的延长线于点M,F是AC1的中点,连结DF.
(猜想)如图①,∠FDM的大小为 度.
(探究)如图②,过点A作AM1∥DF交MD的延长线于点M1,连结BM.求证:△ABM≌△ADM1.
(拓展)如图③,连结AC,若正方形ABCD的边长为2,则△ACC1面积的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com