
【题目】如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )

A.△DEF是等边三角形
B.△ADF≌△BED≌△CFE
C.DE=![]() AB
AB
D.S△ABC=3S△DEF
【答案】C
【解析】
求出∠BDE=∠FEC=∠AFD=30°,求出∠DEF=∠DFE=∠EDF=60°,推出DF=DE=EF,即可得出等边三角形DEF,根据全等三角形性质推出三个三角形全等即可.求出AB=3BE,DE=![]() BE,即可判断选项C.根据相似三角形的面积比等于相似比的平方即可判断选项D.
BE,即可判断选项C.根据相似三角形的面积比等于相似比的平方即可判断选项D.
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠C=∠A=60°,
∵DE⊥BC、EF⊥AC、FD⊥AB,
∴∠DEB=∠EFC=∠FDA=90°,
∴∠BDE=∠FEC=∠AFD=30°,
∴∠DEF=∠DFE=∠EDF=180°﹣90°﹣30°=60°,
∴DF=DE=EF,
∴△DEF是等边三角形,
在△ADF、△BED、△CFE中

∴△ADF≌△BED≌△CFE,
∴AD=BE=CF,
∵∠DEB=90°,∠BDE=30°,
∴BD=2BE,DE=![]() BE,
BE,
∴AB=3BE,
即![]() DE=AB,
DE=AB,
即DE=![]() AB错误;
AB错误;
∵△ABC和△DEF是等边三角形,
∴△ABC∽△DEF,
∴S△ABC:S△DEF=(AB)2:(DE)2=(![]() DE)2:DE2=3,
DE)2:DE2=3,
即只有选项C错误;选项A、B、D正确.
故选C.



 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】学习了相似三角形的知识后,爱探究的小明下晚自习后利用路灯的光线去测量了一路灯的高度,并作出了示意图:如图,路灯(点P)距地面若干米,身高1.6米的小明站在距路灯的底部(O点)20米的A点时,身影的长度AM为5米;
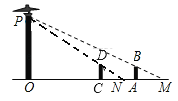
(1)请帮助小明求出路灯距地面的高度;
(2)若另一名身高为1.5米小龙站在直线OA上的C点时,测得他与小明的距离AC为7米,求小龙的身影的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,a≠0,c>0)的自变量x与函数值y的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | p | t | n | t | 0 | … |
有下列结论:①b>0;②关于x的方程ax2+bx+c=0的两个根是0和3;③p+2t<0;④m(am+b)≤﹣4a﹣c(m为任意实数).其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
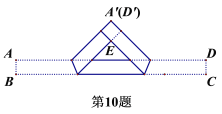
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,![]() //
//![]() ,且分别交对角线AC于点E,F,连接BE,DF.
,且分别交对角线AC于点E,F,连接BE,DF.
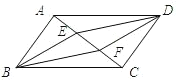
(1)求证:AE=CF;
(2)若BE=DE,求证:四边形EBFD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
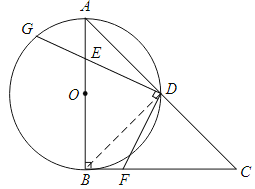
【题目】如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接EF,求证:∠FEB=∠GDA;
(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
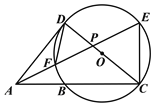
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
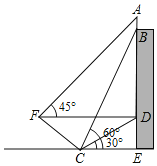
【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度![]() ,他站在距离教学楼底部
,他站在距离教学楼底部![]() 处6米远的地面
处6米远的地面![]() 处,测得宣传牌的底部
处,测得宣传牌的底部![]() 的仰角为
的仰角为![]() ,同时测得教学楼窗户
,同时测得教学楼窗户![]() 处的仰角为
处的仰角为![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度![]() 的斜坡从
的斜坡从![]() 走到
走到![]() 处,此时
处,此时![]() 正好与地面
正好与地面![]() 平行.
平行.
(1)求点![]() 到直线
到直线![]() 的距离(结果保留根号);
的距离(结果保留根号);
(2)若小明在![]() 处又测得宣传牌顶部
处又测得宣传牌顶部![]() 的仰角为
的仰角为![]() ,求宣传牌的高度
,求宣传牌的高度![]() (结果精确到0.1米,
(结果精确到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
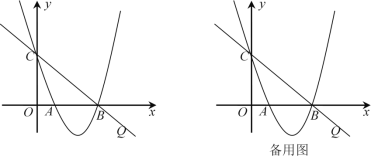
【题目】已知抛物线![]() 过点A(1,0),B(3,0)两点,与y轴交于点C,
过点A(1,0),B(3,0)两点,与y轴交于点C,![]() .
.
(1)求抛物线的解析式;
(2)点![]() 为抛物线在直线
为抛物线在直线![]() 下方图形上的一动点,当
下方图形上的一动点,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为线段
为线段![]() 上的一动点,问:
上的一动点,问:![]() 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由
是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com