
分析 (1)若方程有两个不相等的实数根,则应有△=b2-4ac>0,故计算方程的根的判别式即可证明方程根的情况;
(2)直接代入x=1,求得m的值后,解方程即可求得另一个根.
解答 证明:(1)∵a=1,b=-(2m+1),c=m2+m,
∴△=[-(2m+1)]2-4×1×(m2+m)=1,
∴△>0,
∴关于x的方程x2-(2m+1)x+m2+m=0恒有两个不相等的实数根.
(2)把x=1代入原方程得,1-(2m+1)+m2+m=0,
解得m=0或1,
当m=0时,原方程化为x2-x=0,
解得:x1=0,x2=1,即另一个根为x=0;
当m=1时,原方程化为x2-3x+2=0,
解得:x1=2,x2=1,即另一个根为x=2.
点评 本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0方程有两个不相等的实数根;(2)△=0方程有两个相等的实数根;(3)△<0方程没有实数根.也考查了一元二次方程的解法.


科目:初中数学 来源: 题型:选择题
 小明乘坐摩天轮转一圈,他距离地面的高度y(米)与旋转时间x(分)之间的关系可以近似地用二次函数来刻画.经侧试得部分数据如下表:
小明乘坐摩天轮转一圈,他距离地面的高度y(米)与旋转时间x(分)之间的关系可以近似地用二次函数来刻画.经侧试得部分数据如下表:| x/分 | … | 2.66 | 3.23 | 3.46 | … |
| y/米 | … | 69.16 | 69.62 | 68.46 | … |
| A. | 7分 | B. | 6.5分 | C. | 6分 | D. | 5.5分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
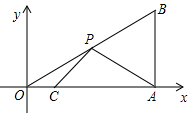 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,$\sqrt{3}$),点C的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,求PA+PC的最小值.
如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,$\sqrt{3}$),点C的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,求PA+PC的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
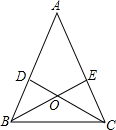 如图,在△ABC中,AB=AC,∠ABC的平分线BE与AC交于点E,∠ACB的平分线CD与AB交于点D,BE与CD相交于点O,求证:OB=OC,OD=OE.
如图,在△ABC中,AB=AC,∠ABC的平分线BE与AC交于点E,∠ACB的平分线CD与AB交于点D,BE与CD相交于点O,求证:OB=OC,OD=OE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2+bx+c=0 | B. | $\frac{1}{x^2}$+x=2 | C. | x2+2x=x2-1 | D. | 3x2+1=2x+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=3,c=2,d=4 | B. | a=4,b=6,c=5,d=10 | ||
| C. | a=2,b=4,c=3,d=6 | D. | a=2,b=3,c=4,d=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com