练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
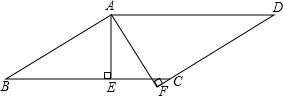
    6．如图，在?ABCD中，AE⊥BC于E，AF⊥DC交DC的延长线于点F，且∠EAF=60°，则∠B等于（　　）
    A．60°B．50°C．70°D．65°

    分析 利用平行四边形的性质以及互余两角的关系求出∠B的度数即可．

    解答 解：∵在?ABCD中，AF⊥CD，
    ∴BA⊥AF，
    ∴∠BAF=90°，
    ∵∠EAF=60°，
    ∴∠BAE=30°，
    ∵AE⊥BC，
    ∴∠B=90°-30°=60°．
    故选：A．

    点评 此题主要考查了平行四边形的性质以及互余两角的关系；熟记平行四边形的性质，求出∠BAE是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．用因式分解法解一元二次方程x（x-3）=x-3时，原方程可化为（　　）
    A．（x-1）（x-3）=0B．（x+1）（x-3）=0C．x （x-3）=0D．（x-2）（x-3）=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列运算中错误的是（　　）
    A．$\sqrt{2}×\sqrt{3}=\sqrt{6}$B．$2\sqrt{2}+3\sqrt{2}=5\sqrt{2}$C．$\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$D．$\sqrt{{{（\sqrt{2}-\sqrt{3}）}^2}}=\sqrt{2}-\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：
    （1）$\sqrt{1\frac{7}{9}}$+$\sqrt{|{-16}|}$；   
    （2）$2\sqrt{2}+3\sqrt{5}-5\sqrt{2}-3\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．在一个不透明的袋中装有除颜色外其余都相同的3个小球，其中一个白球、两个红球．如果一次从袋中摸出两个球，那么摸出的两个球都是红球的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）3x3•x9+x2•x10-2x•x3•x8
    （2）（-a2）3+（-a3）2-a2•a3
    （3）（p-q）4•（q-p）3•（p-q）2    
    （4）（-2x2）3+x2•x4-（-3x3）2
    （5）已知以am=2，an=4，求a3m+2n的值．
    （6）已知a2n=4，b2n=9，求an•bn的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

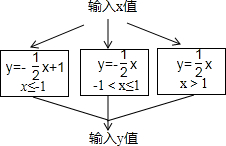    18．根据如图所示的程序计算函数值，若输入的x值为$-\frac{3}{2}$，则输出的结果y应为（　　）
    A．$\frac{7}{4}$B．$-\frac{3}{4}$C．$\frac{1}{4}$D．$\frac{9}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

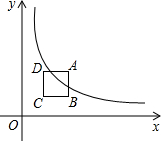    15．在平面直角坐标系的第一象限内，边长为l的正方形ABCD的边均平行于坐标轴，A点的坐标为（a，a）．如图，若曲线y=$\frac{4}{x}$（x＞0）与此正方形的边有交点，则a的取值范围是2≤a≤3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知：如图，在△ABC中，AB=AD=DC，∠BAD=30°；试求∠B和∠C的度数．

    查看答案和解析>>

    同步练习册答案