
【题目】甲、乙两名同学参加少年科技创新选拔赛,六次比赛的成绩如下:
甲:87 93 88 93 89 90
乙:85 90 90 96 89 ![]()
(1)甲同学成绩的中位数是__________;
(2)若甲、乙的平均成绩相同,则![]() __________;
__________;
(3)已知乙的方差是![]() ,如果要选派一名发挥稳定的同学参加比赛,应该选谁?说明理由.
,如果要选派一名发挥稳定的同学参加比赛,应该选谁?说明理由.
【答案】(1)89.5;(2)90;(3)甲,理由见解析.
【解析】
(1)将甲的成绩按照从大到小重新排列,中间两个数的平均数即是中位数;
(2)求出甲的成绩总和得到乙的成绩总和,减去其他成绩即可得到a;
(3)求出甲的平均数,计算出方差,根据甲、乙的方差大小即可做出选择.
(1)将成绩从大到小重新排列为:93、93、90、89、88、87,
∴中位数为: ![]() ,
,
故答案为:89.5;
(2)∵甲、乙的平均成绩相同,
∴甲、乙的总成绩相同,
∴a=(87+93+88+93+89+90)-(85+90+90+96+89)=90;
故答案为:90;
(3)先甲,理由如下:
甲的平均数![]() =
=![]() =90,
=90,
甲的方差S2=![]() =
=![]() ,
,
∵![]() >
>![]() ,
,
∴甲发挥稳定,应该选甲.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2经过点A(4,0),B(1,0).
(1)求出抛物线的解析式;
(2)点D是直线AC上方的抛物线上的一点,求△DCA面积的最大值;
(3)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
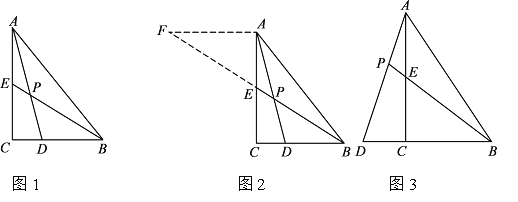
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的函数,自变量
的函数,自变量![]() 的取值范围为
的取值范围为![]() ,下表是
,下表是![]() 与
与![]() 的几组对应值
的几组对应值
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | … |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系中,指出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象.

(2)根据画出的函数图象填空.
①该函数图象与![]() 轴的交点坐标为_____.
轴的交点坐标为_____.
②直接写出该函数的一条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)在函数![]() 中,自变量x的取值范围是________.
中,自变量x的取值范围是________.
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值;
②在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.

(2)结合函数图象写出该函数的一条性质:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个纸盒内有![]() 张完全相同的卡片,分别标号为
张完全相同的卡片,分别标号为![]() ,
,![]() ,
,![]() ,
,![]() .随机抽取一张卡片后不放回,再随机抽取另一张卡片.
.随机抽取一张卡片后不放回,再随机抽取另一张卡片.
(1)用列举法求“两次抽出卡片的标号等于![]() ”的概率;
”的概率;
(2)小明同学连续做了![]() 次试验,这
次试验,这![]() 次试验没有一次出现“两次抽出卡片的标号和等于
次试验没有一次出现“两次抽出卡片的标号和等于![]() ”.他说,“第
”.他说,“第![]() 次试验我一定能够‘两次抽出卡片的标号和等于
次试验我一定能够‘两次抽出卡片的标号和等于![]() ’”.你认为他说得对吗,为什么?
’”.你认为他说得对吗,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校将进行“校春季运动会”,现从全校学生中选出![]() 名同学参加运动会相关服务工作,其中
名同学参加运动会相关服务工作,其中![]() 名男生,
名男生,![]() 名女生.
名女生.
(1)若从这![]() 名同学中随机选取
名同学中随机选取![]() 人作为联络员,求选到男生的概率.
人作为联络员,求选到男生的概率.
(2)若运动会的某项服务工作只在![]() ,
,![]() 两位同学中选一人,准备用游戏的方式决定谁参加.游戏规则是:四个乒乓球上的数字分别为
两位同学中选一人,准备用游戏的方式决定谁参加.游戏规则是:四个乒乓球上的数字分别为![]() ,
,![]() ,
,![]() ,
,![]() (乒乓球只有数字不同,其余完全相同),将乒乓球放在不透明的纸箱中,从中任意摸取两个,若取到的两个乒乓球上的数字之和大于
(乒乓球只有数字不同,其余完全相同),将乒乓球放在不透明的纸箱中,从中任意摸取两个,若取到的两个乒乓球上的数字之和大于![]() 则选
则选![]() ,否则选
,否则选![]() ,从是否公平的角度看,该游戏规则是否合理,用树状图或表格说明理由.
,从是否公平的角度看,该游戏规则是否合理,用树状图或表格说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
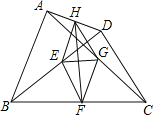
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
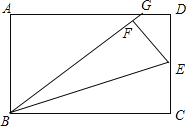
【题目】如图,在矩形ABCD中,点E是CD的中点,将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部,将BF延长交AD于点G.若![]() ,则
,则![]() =__.
=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com