
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
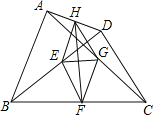
A.1 B.2 C.3 D.4
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学参加少年科技创新选拔赛,六次比赛的成绩如下:
甲:87 93 88 93 89 90
乙:85 90 90 96 89 ![]()
(1)甲同学成绩的中位数是__________;
(2)若甲、乙的平均成绩相同,则![]() __________;
__________;
(3)已知乙的方差是![]() ,如果要选派一名发挥稳定的同学参加比赛,应该选谁?说明理由.
,如果要选派一名发挥稳定的同学参加比赛,应该选谁?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数![]() 的图象过点
的图象过点![]() .直线
.直线![]() 沿y轴平行移动,与x轴,y轴分别交于点B,C,与直线OA交于点D.
沿y轴平行移动,与x轴,y轴分别交于点B,C,与直线OA交于点D.
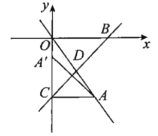
(1)若点D在线段OA上(含端点),求b的取值范围;
(2)当点A关于直线BC的对称点A恰好落在y轴上时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 在线段
在线段![]() 上从
上从![]() 向
向![]() 运动,同时点
运动,同时点![]() 在线段
在线段![]() 上从点
上从点![]() 向
向![]() 运动,速度都是1个单位/秒,时间是
运动,速度都是1个单位/秒,时间是![]() (
(![]() ),连接
),连接![]() 、
、![]() 、
、![]() .
.

(1)请判断![]() 形状,并证明你的结论.
形状,并证明你的结论.
(2)以![]() 、
、![]() 、
、![]() 、
、![]() 四点组成的四边形面积是否发生变化?若不变,求出这个值:若变化,用含
四点组成的四边形面积是否发生变化?若不变,求出这个值:若变化,用含![]() 的式子表示.
的式子表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
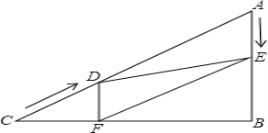
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个动点到达终点时,另一个动点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)当t为何值时,DF=DA?
(2)当t为何值时,△ADE为直角三角形?请说明理由.
(3)是否存在某一时刻t,使点F在线段AC的中垂线上,若存在,请求出t值,若不存在,请说明理由.
(4)请用含有t式子表示△DEF的面积,并判断是否存在某一时刻t,使△DEF的面积是△ABC面积的![]() ,若存在,请求出t值,若不存在,请说明理由.
,若存在,请求出t值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(10.0)及在第一象限的动点P(x,y),且x+y=12,设△OPA的面积为S。
(1)求S关于x的函数解析式;
(2)求x的取值范围;
(3)当S=15时,求P点坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com