
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是BC边上一点,BN⊥AD交AD的延长线于点N. 
(1)如图1,若CM∥BN交AD于点M.
①直接写出图1中所有与∠MCD相等的角:;(注:所找到的相等关系可以直接用于第②小题的证明过程
②过点C作CG⊥BN,交BN的延长线于点G,请先在图1中画出辅助线,再回答线段AM、CG、BN有怎样的数量关系,并给予证明 .
(2)如图2,若CM∥AB交BN的延长线于点M.请证明:∠MDN+2∠BDN=180°.
【答案】
(1)∠CAD,∠CBN;在图1中画出图形,如图所示, 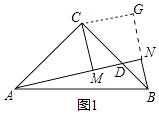
结论:AM=CG+BN,
证明:在△ACM和△BCG中,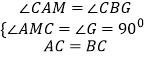 ,
,
∴△ACM≌△BCG,
∴CM=CG,AM=BG,
∵∠CMN=∠MNG=∠G=90°,
∴四边形MNGC是矩形,
∴CM=GN=CG,
∴AM=BG=BN+GN=BN+CG
(2)解:过点C作CE平分∠ACB,交AD于点E.

∵在△ACD和△BDN中,∠ACB=90°,AN⊥ND
∴∠4+∠ADC=90°=∠5+∠BDN
又∵∠ADC=∠BDN
∴∠4=∠5,
∵∠ACB=90°,AC=BC,CE平分∠ACB,
∴∠6=45°,∠2=∠3=45°
又∵CM∥AB,
∴∠1=∠6=45°=∠2=∠3,
在△ACE和△BCM中,
 ,
,
∴△ACE≌△BCM(ASA)
∴CE=CM
又∵∠1=∠2,CD=CD
∴∠CDE=∠CDM
又∵∠BDN=∠CDE,∠MDN+∠CDE+∠CDM=180°
∴∠MDN+2∠BDN=180°
【解析】解:(1)①∵CM∥BN,BN⊥AN,
∴∠CMD=∠N=90°,∠MCD=∠CBN,
∵∠ACB=90°,
∴∠ACM+∠CAD=90°,∠MCD+∠ACM=90°,
∴∠MCD=∠CAD,
所以答案是∠CAD、∠CBN.
②在图1中画出图形,如图所示,
结论:AM=CG+BN,
证明:在△ACM和△BCG中,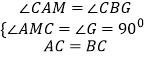 ,
,
∴△ACM≌△BCG,
∴CM=CG,AM=BG,
∵∠CMN=∠MNG=∠G=90°,
∴四边形MNGC是矩形,
∴CM=GN=CG,
∴AM=BG=BN+GN=BN+CG.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 平行四边形的对角线互相垂直 B. 菱形的对角线相等
C. 矩形的对角线互相垂直 D. 正方形的对角线互相垂直且相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A. 形状相同的两个三角形是全等形
B. 面积相等的两个三角形全等
C. 周长相等的两个三角形全等
D. 周长相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点F是AC边上一点,延长BC到点D,使BF=DF,若CD=CF,求证: 
(1)点F为AC的中点;
(2)过点F作FE⊥BD,垂足为点E,请画出图形并证明BD=6CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某粮店出售三种品牌的大米,袋上分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,其中任意拿出两袋,它们最多相差kg.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 两个全等三角形成轴对称
B. 两个三角形关于某直线对称,不一定全等
C. 线段AB的对称轴垂直平分AB
D. 直线MN垂直平分线段AB,则直线MN是线段AB的对称轴
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=ax﹣3a,二次函数y2=x2﹣(a2﹣2)x﹣3.若x>0时,y1y2≥0恒成立,则a的取值范围是( )
A.a≤﹣2或a≥2B.﹣2≤a≤2且a≠0
C.a=﹣2D.a=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com