
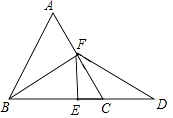
【题目】如图,在等边△ABC中,点F是AC边上一点,延长BC到点D,使BF=DF,若CD=CF,求证: 
(1)点F为AC的中点;
(2)过点F作FE⊥BD,垂足为点E,请画出图形并证明BD=6CE.
【答案】
(1)解:∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∵CF=CD,
∴∠CFD=∠D,
∴∠ACB=2∠D,即∠D= ![]() ∠ACB=30°,
∠ACB=30°,
∵FB=FD,
∴∠FBD=∠D=30°,
∴BF平分∠ABC,
∴AF=CF,即点F为AC的中点
(2)解:如图,
在Rt△EFC中,CF=2CE,
而CD=CF,
∴CF=2CE,
在Rt△BCF中,BC=2CF,
∴BC=4CE,
∴BD=6CE.
【解析】(1)根据等边三角形的性质得∠ABC=∠ACB=60°,利用∠CFD=∠D,则根据三角形外角性质得到∠ACB=2∠D,即∠D= ![]() ∠ACB=30°,然后利用FB=FD得到∠FBD=∠D=30°,则BF平分∠ABC,于是根据等边三角形的性质可得到点F为AC的中点;(2)如图,过点F作FE⊥BD于E,利用含30度的直角三角形三边的关系得到CF=2CE,而CD=CF,则CF=2CE,再利用BC=2CF,所以BD=6CE.
∠ACB=30°,然后利用FB=FD得到∠FBD=∠D=30°,则BF平分∠ABC,于是根据等边三角形的性质可得到点F为AC的中点;(2)如图,过点F作FE⊥BD于E,利用含30度的直角三角形三边的关系得到CF=2CE,而CD=CF,则CF=2CE,再利用BC=2CF,所以BD=6CE.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
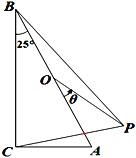
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),∠AOB=120°,在∠AOB内作两条射线OC和OD,且OM平分∠AOD,ON平分∠BOC.
①若∠AOC:∠COD:∠DOB=5:3:4,求∠MON的度数.
②若将图(1)中的∠COD绕点O顺时针转一个小于70°的角α如图(2),其它条件不变,请直接写出∠MON的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是BC边上一点,BN⊥AD交AD的延长线于点N. 
(1)如图1,若CM∥BN交AD于点M.
①直接写出图1中所有与∠MCD相等的角:;(注:所找到的相等关系可以直接用于第②小题的证明过程
②过点C作CG⊥BN,交BN的延长线于点G,请先在图1中画出辅助线,再回答线段AM、CG、BN有怎样的数量关系,并给予证明 .
(2)如图2,若CM∥AB交BN的延长线于点M.请证明:∠MDN+2∠BDN=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
…… ……
按照上述规律排下去,那么第100行从左边数第5个数是( )
A. -4955 B. 4955 C. -4950 D. 4950
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)填空:点B在数轴上表示的数是 ,点C在数轴上表示的数是 ;
(2)若线段CD以每秒3个单位的速度向右匀速运动,当点D运动到A时,线段CD与线段AB开始有重叠部分,此时线段CD运动了 秒;
(3)在(2)的条件下,线段CD继续向右运动,问再经过 秒后,线段CD与线段AB不再有重叠部分;
(4)若线段AB、CD同时从图中位置出发,线段AB以每秒2个单位的速度向左匀速运动,线段CD仍以每秒3个单位的速度向右匀速运动,点P是线段CD的中点,问运动几秒时,点P与线段AB两端点(A或B)的距离为1个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com