

���� ��1����������ֱ��AB��CD�ཻ�ڵ�O����AOC=��AOD���ɵ�ͼ��һ����4��ֱ�ǣ���t=2ʱ������á�MON�Ķ����͡�BON�Ķ�����
��2������OEƽ�֡�COM��OFƽ�֡�NOD����á�COE=$\frac{1}{2}$��COM=$\frac{1}{2}$��15t-90�㣩����DOF=$\frac{1}{2}$��DON=$\frac{1}{2}$��12t���ٸ��ݵ���EOFΪֱ��ʱ����COE+��DOF=90�㣬�г�����$\frac{1}{2}$��15t-90�㣩=$\frac{1}{2}$��12t�����t��ֵΪ10s��
��3�����жϵ�����OM�ڡ�COB�ڲ�����MONΪƽ�ǣ���MOBΪֱ��ʱt��ֵ�����Դ˷�����������ۣ���0��t��$\frac{10}{3}$ʱ����$\frac{10}{3}$��t��6ʱ���ֱ����$\frac{7��COM+2��BON}{��MON}$��ֵ�����ݽ�������жϼ��ɣ�
��� �⣺��1����ͼ��ʾ��������ֱ��AB��CD�ཻ�ڵ�O����AOC=��AOD��
���AOC=��AOD=90�㣬
���BOC=��BOD=90�㣬
��ͼ��һ����4��ֱ�ǣ�
��t=2ʱ����BOM=30�㣬��NON=24�㣬
���MON=30��+90��+24��=144�㣬
��BON=90��+24��=114�㣻
�ʴ�Ϊ��4��144�㣬114�㣻
��2����ͼ��ʾ����BOM=15t����NON=12t����COM=15t-90�㣬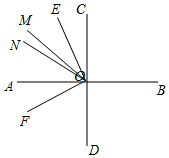
��OEƽ�֡�COM��OFƽ�֡�NOD��
���COE=$\frac{1}{2}$��COM=$\frac{1}{2}$��15t-90�㣩����DOF=$\frac{1}{2}$��DON=$\frac{1}{2}$��12t��
�ߵ���EOFΪֱ��ʱ����COE+��DOF=90�㣬
��$\frac{1}{2}$��15t-90�㣩=$\frac{1}{2}$��12t��
���t=10��
�൱��EOFΪֱ��ʱ��t��ֵΪ10s��
��3������MON=180��ʱ����BOM+��BOD+��DON=180�㣬
��15t+90��+12t=180�㣬
���t=$\frac{10}{3}$��
����BOM=90��ʱ��15t=90�㣬
���t=6��
����ͼ��ʾ����0��t��$\frac{10}{3}$ʱ��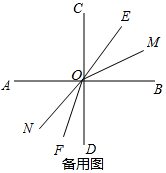
��COM=90��-15t����BON=90��+12t��
��MON=��BOM+��BOD+��DON=15t+90��+12t��
��$\frac{7��COM+2��BON}{��MON}$=$\frac{7��90��-15t��+2��90��+12t��}{15t+90��+12t}$=$\frac{810��-81t}{27t+90��}$�������Ƕ�ֵ��
����ͼ��ʾ����$\frac{10}{3}$��t��6ʱ��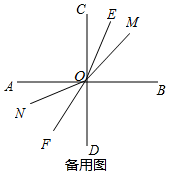
��COM=90��-15t����BON=90��+12t��
��MON=360��-����BOM+��BOD+��DON��=360��-��15t+90��+12t��=270��-27t��
��$\frac{7��COM+2��BON}{��MON}$=$\frac{7��90��-15t��+2��90��+12t��}{270��-27t}$=$\frac{810��-81t}{270��-27t}$=3�����Ƕ�ֵ��
����������������OM�ڡ�COB�ڲ�����$\frac{7��COM+2��BON}{��MON}$�Ƕ�ֵʱ��t��ȡֵ��ΧΪ$\frac{10}{3}$��t��6�������ֵ��3��
���� �������ڼ��α任�ۺ��⣬��Ҫ�����˽ǵĺͲ��ϵ�ļ��㣬�������Ĺؼ��ǽ���صĽ��ú�t�Ĵ���ʽ��ʾ�����������������г����̽�����⣬�Լ����з������ۣ�����ʱע�ⷽ��˼��ͷ���˼���������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
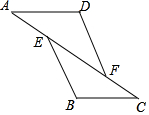 ��ͼ����֪AE=CF����A=��C����ô��������һ�������������ж���ADF�ա�CBE���ǣ�������
��ͼ����֪AE=CF����A=��C����ô��������һ�������������ж���ADF�ա�CBE���ǣ�������| A�� | ��D=��B | B�� | BE=DF | C�� | AD=CB | D�� | BE��DF |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����IΪ��ABC�����ģ���OΪ��ABC�����ģ�����BIC=140�㣬���BOC=160�㣮
��ͼ����IΪ��ABC�����ģ���OΪ��ABC�����ģ�����BIC=140�㣬���BOC=160�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����������a��b�������ϵĶ�Ӧ���λ����ͼ��ʾ�������и�ʽ������ǣ�������
��ͼ����������a��b�������ϵĶ�Ӧ���λ����ͼ��ʾ�������и�ʽ������ǣ�������| A�� | $\frac{|a|}{a}$+$\frac{|b|}{b}$=0 | B�� | a+b��0 | C�� | |a+b|-a=b | D�� | -b��a��-a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����Pλ�ڵ�O�ģ�������
��ͼ����Pλ�ڵ�O�ģ�������| A�� | ��ƫ��32�� | B�� | ��ƫ��32�� | C�� | ��ƫ��58�� | D�� | ��ƫ��58�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ѡ�QQ��Ц������ֱ������ϵ�У���֪����A�������ǣ�-2��3�����촽C�������Ϊ��-1��1������ˡ�QQ��Ц������B�������ǣ�������
��ͼ���ѡ�QQ��Ц������ֱ������ϵ�У���֪����A�������ǣ�-2��3�����촽C�������Ϊ��-1��1������ˡ�QQ��Ц������B�������ǣ�������| A�� | ��0��3�� | B�� | ��0��1�� | C�� | ��-1��2�� | D�� | ��-1��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����7 | B�� | ��7 | C�� | ����7 | D�� | ������7 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com