
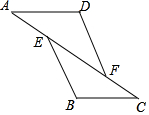
 如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )| A. | ∠D=∠B | B. | BE=DF | C. | AD=CB | D. | BE∥DF |
分析 利用等式的性质可得AF=CE,再根据全等三角形的判定方法进行分析即可.
解答 解:∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
A、添加∠D=∠B可利用AAS判定△ADF≌△CBE,故此选项不合题意;
B、添加BE=DF不能判定△ADF≌△CBE,故此选项符合题意;
C、添加AD=BC可利用SAS判定△ADF≌△CBE,故此选项不合题意;
D、添加BE∥DF可得∠BEC=∠DFA,可利用ASA判定△ADF≌△CBE,故此选项不合题意;
故选:B.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 一台电风扇 | 一台收音机 | 谢谢参与 |
| 谢谢参与 | 一副球拍 | 一个U盘 |
| 两张电影票 | 谢谢参与 | 一副球拍 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5x+9=4x+15 | B. | 5x-9=4x-15 | C. | 5x-9=4x+15 | D. | 5x+9=4x-15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 根的情况无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com