练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．小明在做数学题时，发现了下面有趣的结果：
    3-2=1
    8+7-6-5=4
    15+14+13-12-11-10=9
    24+23+22+21-20-19-18-17=16
    …
    根据以上规律，可知第20行左起第一个数是440．

    分析 根据左起第一个数3，8，15，24…的变化规律得出第n行左起第一个数为（n+1）2-1，由此求出即可．

    解答 解：∵3=22-1，
    8=32-1，
    15=42-1，
    24=52-1，
    …
    ∴第20个式子左起第一个数是：212-1=440．
    故答案为：440．

    点评 此题主要考查了数字变化规律，根据已知得出数字的变与不变是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

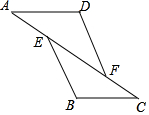    17．如图，已知AE=CF，∠A=∠C，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（　　）
    A．∠D=∠BB．BE=DFC．AD=CBD．BE∥DF

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，把“QQ”笑脸放在直角坐标系中，已知右眼A的坐标是（-2，3），嘴唇C点的坐标为（-1，1），则此“QQ”笑脸左眼B的坐标是（　　）
    A．（0，3）B．（0，1）C．（-1，2）D．（-1，3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，在直角△ABC中，斜边AB上的垂直平分线交直角边BC于D，交AB于E，若BC=10cm，AC=6cm，则△ADC的周长为16cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．先化简，再求代数式：$\frac{x+1}{x}$÷（$\frac{{x}^{2}+1}{2x}$-x）的值，其中x=2sin 60°+2cos60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知：如图①，在平行四边形ABCD中，AB=3cm，BC=5cm，AC⊥AB．△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿着CB方向匀速移动，速度为1cm/s；当△PNM停止平移时，点Q也停止移动，如图②．设移动时间为t（s）（0＜t＜4）．连接PQ、MQ、MC．解答下列问题：

    （1）当t为何值时，PQ∥AB？
    （2）当t=3时，求△QMC的面积；
    （3）是否存在某一时刻t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．

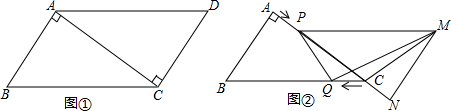
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．直线a上有一点A，直线b上有一点B，且a∥b．点P在直线a，b之间，若PA=3，PB=4，则直线a、b之间的距离（　　）
    A．等于7B．小于7C．不小于7D．不大于7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．某课题组为了解全市九年级学生对数学知识的掌握情况，在一次数学检测中，从全市20000 名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如图表：
    分数段频数频率
    50≤x≤60200.10
    60≤x≤7028b
    70≤x≤80540.27
    80≤x≤90a0.20
    90≤x≤100240.12
    100≤x≤110180.09
    110≤x≤120160.08
    （1）表中a和b所表示的数分别为：a=40，b=0.14；
    （2）请在图中补全额数分布直方图；
    （3）如果把成绩在70分以上（含70分）定为合格，那么该市20000名九年级考生数学成绩为合格的学生约有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，在Rt△ACB中，∠C=90°，AC=16cm，BC=8cm，动点P从点C出发，沿CA方向运动；动点Q同时从点B出发，沿BC方向运动，如果点P的运动速度为4cm/s，Q点的运动速度为2cm/s，那么运动几秒时，△ABC和△PCQ相似？

    查看答案和解析>>

    同步练习册答案