
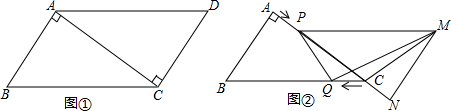
���� ��1�����ݹ��ɶ������AC������PQ��AB���ó�����t�ı���ʽ����⼴�ɣ�
��2������P��PD��BC��D�����ݡ�CPD�ס�CBA���г�����t�ı���ʽ����ʾ��PD�ij����ٸ���S��QMC=$\frac{1}{2}$QC•PD�����м��㼴�ɣ�
��3������M��ME��BC���ӳ����ڵ�E�����ݡ�CPD�ס�CBA���ó�$PD=\frac{3}{5}��4-t��$��$CD=\frac{4}{5}��4-t��$���ٸ��ݡ�PDQ�ס�QEM���õ�$\frac{PD}{QE}=\frac{DQ}{EM}$����PD•EM=QE•DQ�������õ�����${��\frac{12}{5}-\frac{3}{5}t��^2}$=$��\frac{16}{5}-\frac{9}{5}t����\frac{9}{5}+\frac{9}{5}t��$�����$t=\frac{3}{2}$��t=0����ȥ�������ɵó���$t=\frac{3}{2}$ʱ��PQ��MQ��
��� 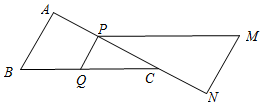 �⣺��1����ͼ��ʾ��AB=3cm��BC=5cm��AC��AB��
�⣺��1����ͼ��ʾ��AB=3cm��BC=5cm��AC��AB��
��Rt��ABC��AC=4��
��PQ��AB������$\frac{CP}{PA}=\frac{CQ}{QB}$��
��CQ=PA=t��CP=4-t��QB=5-t��
��$\frac{4-t}{t}=\frac{t}{5-t}$��
��20-9t+t2=t2��
���$t=\frac{20}{9}$��
��$t=\frac{20}{9}$ʱ��PQ��AB��
��2����ͼ��ʾ������P��PD��BC�ڵ�D��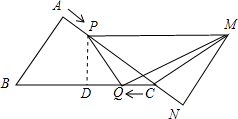
���PDC=��A=90�㣬
�ߡ�PCD=��BCA
���CPD�ס�CBA��
��$\frac{CP}{CB}=\frac{PD}{BA}$��
��t=3ʱ��CP=4-3=1��
��BA=3��BC=5��
��$\frac{1}{5}=\frac{PD}{3}$��
��$PD=\frac{3}{5}$��
�֡�CQ=3��PM��BC��
��${S_{��QMC}}=\frac{1}{2}��3��\frac{3}{5}=\frac{9}{10}$��
��3������ʱ��$t=\frac{3}{2}$��ʹPQ��MQ��
�������£���ͼ��ʾ������M��ME��BC���ӳ����ڵ�E��
�ߡ�CPD�ס�CBA��
��$\frac{CP}{CB}=\frac{PD}{BA}=\frac{CD}{CA}$��
��BA=3��CP=4-t��BC=5��CA=4��
��$\frac{4-t}{5}=\frac{PD}{3}=\frac{CD}{4}$��
��$PD=\frac{3}{5}��4-t��$��$CD=\frac{4}{5}��4-t��$��
��PQ��MQ��
���PDQ=��QEM=90�㣬��PQD=��QME��
���PDQ�ס�QEM��
��$\frac{PD}{QE}=\frac{DQ}{EM}$����PD•EM=QE•DQ��
��$EM=PD=\frac{3}{5}��4-t��=\frac{12}{5}-\frac{3}{5}t$��
$DQ=CD-CQ=\frac{4}{5}��4-t��-t=\frac{16}{5}-\frac{9}{5}t$��
$QE=DE-DQ=5-[\frac{4}{5}��4-t��-t]=\frac{9}{5}+\frac{9}{5}t$��
��${��\frac{12}{5}-\frac{3}{5}t��^2}$=$��\frac{16}{5}-\frac{9}{5}t����\frac{9}{5}+\frac{9}{5}t��$��
��2t2-3t=0��
��$t=\frac{3}{2}$��t=0����ȥ����
�൱$t=\frac{3}{2}$ʱ��PQ��MQ��
���� ���������ı����ۺ��⣬��Ҫ���������������ε��ж������ʡ����ɶ�����ƽ���ߵ����ʡ������ε����������ۺ�Ӧ�ã��������Ĺؼ��Ǹ������⻭��ͼ�Σ����������ߣ��������������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5x+9=4x+15 | B�� | 5x-9=4x-15 | C�� | 5x-9=4x+15 | D�� | 5x+9=4x-15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
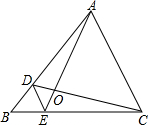 ��ͼ��D��E�ֱ��ǡ�ABC�ı�AB��BC�ϵĵ㣬��DE��AC����S��DOE��S��AOC=1��16����S��BDE��S��CDE���ڣ�������
��ͼ��D��E�ֱ��ǡ�ABC�ı�AB��BC�ϵĵ㣬��DE��AC����S��DOE��S��AOC=1��16����S��BDE��S��CDE���ڣ�������| A�� | 1��5 | B�� | 1��4 | C�� | 1��3 | D�� | 1��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��O������A�ľ�����ڵ�����B�ľ��� | |
| B�� | ��O������A�ľ�����ڵ�����B�ľ��� | |
| C�� | ��O����AB�ľ�����ڵ���BC�ľ��� | |
| D�� | ��O����AB�ľ�����ڵ���BC�ľ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2 | B�� | y1=y2 | C�� | y1��y2 | D�� | ���ܱȽ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com