练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．若一个一元二次方程的两个根分别是1、3，请写出一个符合题意的一元二次方程x2-4x+3=0．

    分析 先计算出1与3的和、积，然后根据根与系数的关系写出满足条件的一元二次方程．

    解答 解：∵1+3=4，1×3=3，
    ∴以1和3为根的一元二次方程可为x2-4x+3=0．
    故答案为x2-4x+3=0．

    点评 本题考查了根与系数的关系．一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系为：x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．如图是一个圆柱体，则从正上方看到的图形是（　　）
    A．等腰三角形B．等边三角形C．一个点D．圆

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，已知线段AB=60，点C、D分别是线段AB上的两点，且满足AC：CD：DB=3：4：5，点K是线段CD的中点，求线段KB的长．
    解：设AC=3x，则CD=4x，DB=5x，
    ∵AB=AC+CD+DB=60
    ∴AB=3x+4x+5x（用含x的代数式表示）=60．
    ∴x=5．
    ∵点K是线段CD的中点．
    ∴KD=$\frac{1}{2}$CD=10．
    ∴KB=KD+DB=35．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图扇形OAB中，C是$\widehat{AB}$上一动点（不与A，B重合），CD┴OB于D，P为△COD的内心，则∠BPO为（　　）
    A．120°B．135°C．150°D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在图中，你能量出点A到BC边所在直线的距离吗？（先作图，再度量）
    表述为：过点A作AD⊥直线BC交BC的延长线于点D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．当a=2时，其值为零的分式是（　　）
    A．$\frac{a-2}{（a-2）^{2}}$B．$\frac{2a-4}{a-1}$C．$\frac{1}{a-2}$D．$\frac{a+2}{2a}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．单项式$\frac{12}{5}$πR2的系数是$-\frac{12}{5}{π^{\;}}$，次数是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算：
    （1）-12014-$\root{3}{27}$×（-$\frac{1}{2}$）-2+（π-$\sqrt{2}$）0-|-4|+$\sqrt{9}$
    （2）（a2b-2ab2-b3）÷b-（a+b）（a-b）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

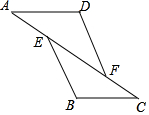    17．如图，已知AE=CF，∠A=∠C，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（　　）
    A．∠D=∠BB．BE=DFC．AD=CBD．BE∥DF

    查看答案和解析>>

    同步练习册答案