
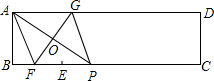
 如图,矩形ABCD中,AD=7,AB=BE=2,点P是EC(包括E、C)上的动点,线段AP的垂直平分线分别交BC、AD于点F、G,设BP=x,AG=y.
如图,矩形ABCD中,AD=7,AB=BE=2,点P是EC(包括E、C)上的动点,线段AP的垂直平分线分别交BC、AD于点F、G,设BP=x,AG=y.分析 (1)首先根据全等三角形判定的方法,判断出△AOG≌△POF,即可判断出OG=OF;然后判断出AP、GF互相垂直平分,即可推得四边形AFPG是菱形.
(2)首先根据四边形AFPG是菱形,可得AF=PF=AG=y;然后根据BF=BP-PF=x-y,在Rt△ABF中,应用勾股定理,求出y与x的函数关系式即可.
(3)首先设以线段GP、DC为直径的圆的圆心分别是点M、N,则MN∥AD∥BC,据此求出MN的值是多少;然后判断出以线段GP、DC为直径的圆的半径分别是$\frac{x}{2}$、1,再根据两圆外切,可得MN=$\frac{x}{2}$+1,据此求出x的值是多少即可.
解答 解:(1)四边形AFPG是菱形.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OAG=∠OPF,
∵FG是线段AP的垂直平分线,
∴AO=PO,∠AOG=∠POF=90°,
在△AOG和△POF中,
$\left\{\begin{array}{l}{∠OAG=∠OPF}\\{AO=PO}\\{∠AOG=∠POF}\end{array}\right.$,
∴△AOG≌△POF,
∴OG=OF,
∴AP、GF互相垂直平分,
∴四边形AFPG是菱形.
(2)∵四边形AFPG是菱形,
∴AF=PF=AG=y,
又∵BP=x,
∴BF=BP-PF=x-y,
在Rt△ABF中,
BF2=AF2-AB2=y2-22=(x-y)2,
整理,可得y=$\frac{x}{2}$+$\frac{2}{x}$.
(3)如图1,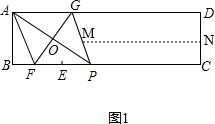 ,
,
设以线段GP、DC为直径的圆的圆心分别是点M、N,
则MN∥AD∥BC,
∴MN=$\frac{1}{2}(GD+PC)$=$\frac{1}{2}$[(7-x)+(7-$\frac{x}{2}$-$\frac{2}{x}$)]=7-$\frac{3}{4}x$-$\frac{1}{x}$,
∵GP=x,CD=2,
∴以线段GP、DC为直径的圆的半径分别是$\frac{x}{2}$、1,
当以线段GP、DC为直径的两圆外切时,
7-$\frac{3}{4}x$-$\frac{1}{x}$=$\frac{x}{2}$+1,
整理,可得
$\frac{5}{4}x+\frac{1}{x}-6=0$,
解得x=$\frac{12+2\sqrt{31}}{5}$或x=$\frac{12-2\sqrt{31}}{5}$,
∵$\frac{12-2\sqrt{31}}{5}$<1,
∴x=$\frac{12-2\sqrt{31}}{5}$不符合题意,
∴x=$\frac{12+2\sqrt{31}}{5}$.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了数形结合思想的应用,考查了空间想象的能力的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.
(3)此题还考查了菱形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①菱形具有平行四边形的一切性质;②菱形的四条边都相等; ③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
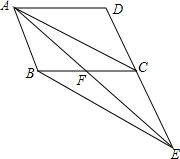 如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于F.
如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=1,BC=$\sqrt{2}$,CD=5,AD=2$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=1,BC=$\sqrt{2}$,CD=5,AD=2$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com