练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．若m+$\frac{1}{m}$=$\sqrt{5}$，则非负数m-$\frac{1}{m}$的平方根是（　　）
    A．±2B．±1C．1D．2

    分析 把已知等式两边平方，求出m2+$\frac{1}{{m}^{2}}$的值，再利用完全平方公式即可求出所求式子的平方根．

    解答 解：把m+$\frac{1}{m}$=$\sqrt{5}$，两边平方得：m2+$\frac{1}{{m}^{2}}$+2=5，即m2+$\frac{1}{{m}^{2}}$=3，
    ∴（m-$\frac{1}{m}$）2=m2+$\frac{1}{{m}^{2}}$-2=1，即m-$\frac{1}{m}$=1，
    则非负数m-$\frac{1}{m}$的平方根是±1，
    故选B．

    点评 此题考查了完全平方公式，以及平方根，熟练掌握完全平方公式是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．随着车辆的增加，交通违规的现象越来越严重，交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理（速度在30-40含起点值30，不含终点值40），得到其频数及频率如表：
    数据段频数频率
    30-40100.05
    40-5036c
    50-60a0.39
    60-70bd
    70-80200.10
    总计2001
    （1）表中a、b、c、d分别为：a=78； b=56； c=0.18； d=0.28
    （2）补全频数分布直方图；
    （3）如果汽车时速不低于60千米即为违章，则违章车辆共有多少辆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如果xy≠0，$\frac{1}{3}$xy2+axy2=0，那么a的值为（　　）
    A．0B．3C．-3D．-$\frac{1}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如果$\frac{x}{y}$=$\frac{7}{3}$，那么$\frac{x-y}{y}$=$\frac{4}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．在△ABC中，cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$，cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$，cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$，我们称为余弦定理，请用余弦定理完成下面的问题．请用余弦定理完成下面的问题：
    （1）如图，已知△DEF，∠E=60°，DE=4，DF=$\sqrt{13}$，求EF的长度；
    （2）通过合理的构造，试求cos105°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

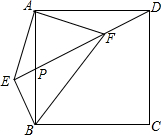    4．如图，在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE，FA⊥AE交DP于点F，连接BF、FC．若AE=4，则FC=4$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，已知四边形ABCD为正方形，过顶点A的直线交正方形ABCD边CD于点E．
    （1）如图①，若∠DAE=30°，M为AE的中点，过点M的直线PQ⊥AE，且PQ与AD，BC分别相交于点P，Q．求证：PQ=AE；
    （2）如图②，若AE交CD于点E，DF⊥AE于F，点O为对角线AC的中点，在AE上截取AG=DF，连接OF，OG，那么△OFG是哪种特殊三角形，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．$\frac{1}{3}$πR2的系数是$\frac{1}{3}π$，次数是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）5$\sqrt{\frac{1}{5}}$+$\frac{1}{2}$$\sqrt{20}$-$\frac{5}{2}$$\sqrt{\frac{1}{5}}$+$\sqrt{45}$-$\frac{1}{2}$$\sqrt{405}$     
    （2）12$\sqrt{\frac{1}{6}}$÷3$\sqrt{\frac{7}{12}}$×$\frac{1}{2}$$\sqrt{10\frac{1}{2}}$
    （3）（2$\sqrt{7}$-5$\sqrt{2}$）2-（5$\sqrt{2}$+2$\sqrt{7}$）2
    （4）$\frac{sin60°+tan45°}{cos30°-4si{n}^{2}30°}$．

    查看答案和解析>>

    同步练习册答案