
 在△ABC中,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,我们称为余弦定理,请用余弦定理完成下面的问题.请用余弦定理完成下面的问题:
在△ABC中,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,我们称为余弦定理,请用余弦定理完成下面的问题.请用余弦定理完成下面的问题:分析 (1)运用余弦定理即可求出EF的值;
(2)由余弦定理可构造出△ABC,求解即可.
解答 解:(1)由余弦定理,可得cosE=$\frac{D{E}^{2}+E{F}^{2}-D{F}^{2}}{2DE•EF}$,
∵∠E=60°,DE=4,DF=$\sqrt{13}$,
∴$\frac{1}{2}$=$\frac{16+E{F}^{2}-13}{2×4EF}$,
解得EF=1或3;
(2)如图,在△ABC中,∠B=45°,∠C=30°,AD⊥BC,AD=1.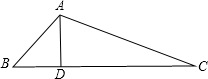
∵在RT△ADC中,AD=1.
∴AC=2,CD=$\sqrt{3}$,
∵在RT△ADB中,AD=1,
∴AB=$\sqrt{2}$,BD=1,
∴在△ABC中,AB=$\sqrt{2}$,AC=2,BC=$\sqrt{3}$+1,
∠BAC=180°-30°-45°=105°,
利用余弦定理可得cos105°=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{2+4-(\sqrt{3}+1)^{2}}{2×\sqrt{2}×2}$=$\frac{\sqrt{2}-\sqrt{6}}{4}$.
点评 本题主要考查了余弦定理,解题的关键是能构灵活运用余弦定理构造出三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±2 | B. | ±1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
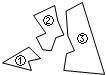 某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带③去,这样做根据的三角形全等判定方法为( )
某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带③去,这样做根据的三角形全等判定方法为( )| A. | S.A.S. | B. | A.S.A. | C. | A.A.S. | D. | S.S.S. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
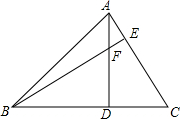 如图,已知AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,DF=DC,则∠ABC的大小是( )
如图,已知AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,DF=DC,则∠ABC的大小是( )| A. | 30度 | B. | 45度 | C. | 60度 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com