
分析 方程的两根为x1,x2,根据根与系数的关系得到x1+x2=-(2k-3),x1•x2=k2-2,根据题意得出方程求得方程解即可.
解答 解:∵关于x的方程x2+(2k-3)x+k2-3=0有两个实数根x1,x2,
∴x1+x2=-(2k-3),x1•x2=k2-3,
∵x1+x2=$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,
∴k2-3=1,
则k=±2.
点评 此题考查根与系数的关系,一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1,x2,则两根与方程系数之间有如下关系:x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
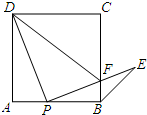 如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.
如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 都有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:| 数据段 | 频数 | 频率 |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | c |
| 50-60 | a | 0.39 |
| 60-70 | b | d |
| 70-80 | 20 | 0.10 |
| 总计 | 200 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
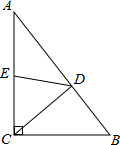 如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,过点C作CD⊥AB,取AC的中点E,连接DE,则△DEC的周长是( )
如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,过点C作CD⊥AB,取AC的中点E,连接DE,则△DEC的周长是( )| A. | 2.4 | B. | 4.4 | C. | 6.4 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,我们称为余弦定理,请用余弦定理完成下面的问题.请用余弦定理完成下面的问题:
在△ABC中,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,我们称为余弦定理,请用余弦定理完成下面的问题.请用余弦定理完成下面的问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com