
分析 ①利润=售价-进价,降低1元增加40件,可知降低x元增加40x件,一件商品的利润乘以销售量得到总利润,可列出方程;
②设每件需降价的钱数为x元,每天获利y元,则可求出y与x之间的函数关系式,写成顶点式后直接解答.
解答 解:①(12.5×0.8-6-x)(100+40x)=420
整理得2x2-3x+1=0,
解得x1=0.5,x2=1,
答:若每天的利润达到420元,则必须降0.5元或1元.
②设每件需降价的钱数为x元,每天获利y元,
则y=(12.5×0.8-6-x)(100+40x)
即:y=-402+60x+400=-40(x-0.75)2+422.5,
当x=0.75元时,y最大为422.5.
即降价0.75元时,利润达到最高,此时的利润为422.5元.
点评 此题考查了一元二次方程和二次函数的应用,掌握销售问题中的基本数量关系是解决问题的关键.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:解答题
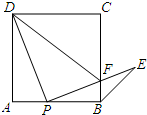 如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.
如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,我们称为余弦定理,请用余弦定理完成下面的问题.请用余弦定理完成下面的问题:
在△ABC中,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,我们称为余弦定理,请用余弦定理完成下面的问题.请用余弦定理完成下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
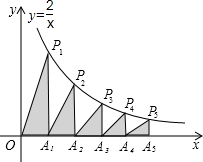 如图,在x轴的正半轴上依次截取OA1=A1A2=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S5的值为$\frac{1}{5}$,以此类推Sn=$\frac{1}{n}$(n≥1的整数)
如图,在x轴的正半轴上依次截取OA1=A1A2=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S5的值为$\frac{1}{5}$,以此类推Sn=$\frac{1}{n}$(n≥1的整数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com