
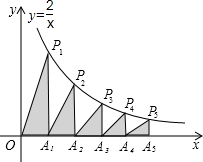
 如图,在x轴的正半轴上依次截取OA1=A1A2=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S5的值为$\frac{1}{5}$,以此类推Sn=$\frac{1}{n}$(n≥1的整数)
如图,在x轴的正半轴上依次截取OA1=A1A2=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S5的值为$\frac{1}{5}$,以此类推Sn=$\frac{1}{n}$(n≥1的整数) 分析 根据反比例函数y=$\frac{k}{x}$中k的几何意义再结合图象即可解答.
解答 解:∵过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,S=$\frac{1}{2}$|k|.
∴S1=1,S△OA2P2=1,
∵OA1=A1A2,
∴$\frac{1}{2}$S△OA2P2=$\frac{1}{2}$,
同理可得,S2=$\frac{1}{2}$S1=$\frac{1}{2}$,S3=$\frac{1}{3}$S1=$\frac{1}{3}$,S4=$\frac{1}{4}$S1=$\frac{1}{4}$,S5=$\frac{1}{5}$S1=$\frac{1}{5}$.
以此类推,Sn=$\frac{1}{n}$.
故答案是:$\frac{1}{5}$,$\frac{1}{n}$.
点评 主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
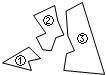 某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带③去,这样做根据的三角形全等判定方法为( )
某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带③去,这样做根据的三角形全等判定方法为( )| A. | S.A.S. | B. | A.S.A. | C. | A.A.S. | D. | S.S.S. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
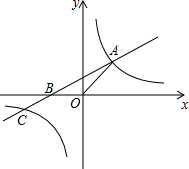 如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=$\frac{4}{x}$交于点A、C,其中点A在第一象限,点C在第三象限.
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=$\frac{4}{x}$交于点A、C,其中点A在第一象限,点C在第三象限.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
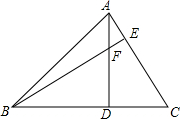 如图,已知AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,DF=DC,则∠ABC的大小是( )
如图,已知AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,DF=DC,则∠ABC的大小是( )| A. | 30度 | B. | 45度 | C. | 60度 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | $\sqrt{3}$-2 | C. | $\sqrt{3}$+2 | D. | -$\sqrt{3}$-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com