
分析 (1)去分母、去括号、移项、合并同类项、系数化成1即可求解;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)去分母,得2(2x-4)>3(3x-1),
去括号,得4x-8>9x-3,
移项,得4x-9x>8-3,
合并同类项,得-5x>5,
系数化成1得x<-1.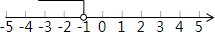 ;
;
(2)$\left\{\begin{array}{l}{5x-1<3(x+1)…①}\\{\frac{x-1}{2}≥1…②}\end{array}\right.$,
解①得:x<2,
解②得:x≥3. ,
,
则不等式组无解.
点评 本题考查了不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
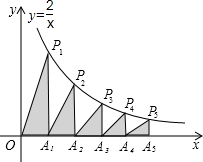 如图,在x轴的正半轴上依次截取OA1=A1A2=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S5的值为$\frac{1}{5}$,以此类推Sn=$\frac{1}{n}$(n≥1的整数)
如图,在x轴的正半轴上依次截取OA1=A1A2=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数的y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4、A4P5A5并设其面积分别为S1、S2、S3、S4、S5,则S5的值为$\frac{1}{5}$,以此类推Sn=$\frac{1}{n}$(n≥1的整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
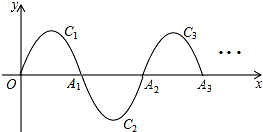 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com