
 如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.
如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.分析 (1)首先令x=0,y=0求出A、B的坐标.然后解直角三角形求得∠OAB=30°,根据勾股定理求出AB的长,继而可求出∠OAC=∠OAB+∠BAC=90°,即可求得C的坐标.
(2)由△ABP和△ABC的面积相等,得到点C与点P到直线AB的距离相等,得到PC∥AB,根据直线AB设出直线PC的解析式,代入C的坐标,根据待定系数法即可求得直线PC的解析式,然后把y=$\frac{1}{2}$代入即可求得.
解答 解:(1)$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴、y轴交于A、B两点,
∴A($\sqrt{3}$,0),B(0,1).
∴OA=$\sqrt{3}$,OB=1,
∵△AOB为直角三角形,
∴AB=2.tan∠OAB=$\frac{OB}{OA}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠OAB=30°,
∵△ABC是等边三角形,
∴∠BAC=60°,AC=AB=2,
∴∠OAC=∠OAB+∠BAC=90°,
∴C($\sqrt{3}$,2);
(2)∵△PAB的面积等于△ABC的面积,
∴点C与点P到直线AB的距离相等,
∴PC∥AB,
设直线PC的解析式为y=-$\frac{\sqrt{3}}{3}$x+b,
把C($\sqrt{3}$,2)代入得,2=-$\frac{\sqrt{3}}{3}$×$\sqrt{3}$+b,
解得b=3,
∴直线PC的解析式为y=-$\frac{\sqrt{3}}{3}$x+3,
把(m,$\frac{1}{2}$)代入得,$\frac{1}{2}$=-$\frac{\sqrt{3}}{3}$m+3,
解得m=$\frac{5\sqrt{3}}{2}$.
∴在第一象限内存在有一点P(m,$\frac{1}{2}$),使△PAB的面积等于△ABC的面积.此时m的值为$\frac{5\sqrt{3}}{2}$.
点评 本题是一次函数的综合题,考查了等边三角形的性质,直角三角形函数,平行线的性质,待定系数法求一次函数的解析式以及一次函数图象上点的坐标特征,根据题意求得∠OAC=∠OAB+∠BAC=90°是解题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
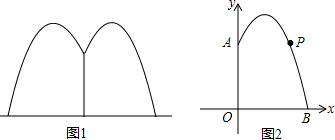
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
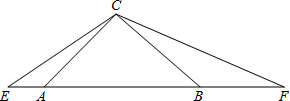 如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.
如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
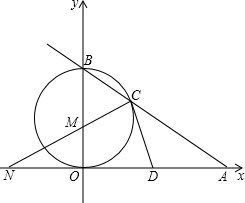 如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.
如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2-mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
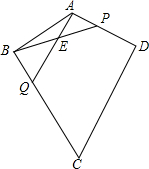 如图,四边形ABCD中,∠C=60°,AB=AD=5,CB=CD=8,点P、Q分别是边AD、BC上的动点,AQ和BP交于点E,且∠BEQ=90°-$\frac{1}{2}$∠BAD,设A、P两点的距离为x.
如图,四边形ABCD中,∠C=60°,AB=AD=5,CB=CD=8,点P、Q分别是边AD、BC上的动点,AQ和BP交于点E,且∠BEQ=90°-$\frac{1}{2}$∠BAD,设A、P两点的距离为x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com