
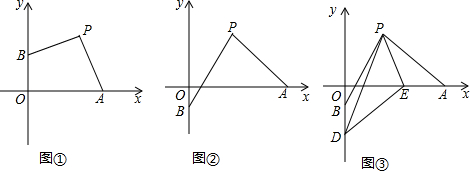
分析 (1)作PM⊥x轴于M,PN⊥y轴于N,求出PN=PM,求出∠NPB=∠APM,∠PNB=∠PMA=90°,证△PNB≌△PMA,推出AM=BN、0M=ON,证0A+OB=OM+ON=8;
(2)如图②过P作PM⊥x轴于M,PN⊥y轴于N,由P(5,5),得到PM=MO=ON=PN=5,由于∠MPB+∠BPN=∠MPN=90°,∠BPN+∠NPA=90°,于是得到∠MPB=∠NPA,推出△PBN≌△APM,根据全等三角形的性质得到AM=BN,即可得到结论;(3)过P作PF⊥PE,由∠DPE=45°,推出PD为∠FPE的平分线,由(1)(2)同理可得,PF=PE,证得△PDF≌△PDE,根据全等三角形的性质得到∠BDP=∠GDP,过P作∠DPQ=∠DPB,由∠APB=90°,∠DPE=∠DPQ+∠EPQ=45°,得到∠OPB=∠EPA=45°,∠EPQ=∠EPA,证得△DPB≌△DPQ,根据全等三角形的性质得到BD=DQ,BP=PQ,由(1)(2)知,PA=PB,求得PQ=PA,推出△PEQ≌△PEA,得到QE=EA,于是得到结论.
解答 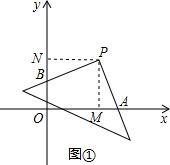 解:(1)如图①,作PM⊥x轴于M,PN⊥y轴于N,
解:(1)如图①,作PM⊥x轴于M,PN⊥y轴于N,
∵P(5,5),
∴PN=PM=5,∠NPM=360°-90°-90°-90°=90°=∠BPA,
∴∠NPB=∠APM,∠PNB=∠PMA=90°,
在△PNB和△PMA中
$\left\{\begin{array}{l}{∠PNB=∠PMA}\\{PN=PM}\\{∠NPB=∠MPA}\end{array}\right.$
∴△PNB≌△PMA(ASA),
∴AM=BN、0M=ON,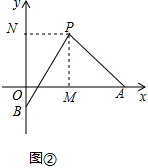
∴0A+OB=OM+ON=10;
(2)如图②,过P作PM⊥x轴于M,PN⊥y轴于N,
∵P(5,5),
∴PM=MO=ON=PN=5,
∵∠MPB+∠BPN=∠MPN=90°,∠BPN+∠NPA=90°,
∴∠MPB=∠NPA,
在△PBN与△APM中,$\left\{\begin{array}{l}{∠NPA=∠MPB}\\{∠PNB=∠AMP}\\{PB=PA}\end{array}\right.$,
∴△PBN≌△APM,
∴AM=BN,
∴OA-OB=(OM+MA)-(NB-NO)=OM+ON=10;
(3)如图③,过P作PF⊥PE,
∵∠DPE=45°,
∴PD为∠FPE的平分线,
由(1)(2)同理可得,PF=PE,
在△PDF与△PDE中,$\left\{\begin{array}{l}{PE=PF}\\{∠FPD=∠EPD}\\{PD=PD}\end{array}\right.$,
∴△PDF≌△PDE,
∴∠BDP=∠GDP,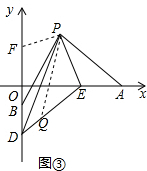
过P作∠DPQ=∠DPB,
∵∠APB=90°,∠DPE=∠DPQ+∠EPQ=45°,
∴∠OPB=∠EPA=45°,∠EPQ=∠EPA,
在△DPB与△DPG中,$\left\{\begin{array}{l}{∠DPQ=∠DPB}\\{PD=PD}\\{∠BDP=∠QDP}\end{array}\right.$,
∴△DPB≌△DPQ,
∴BD=DQ,BP=PQ,
由(1)(2)知,PA=PB,
∴PQ=PA,
在△PEQ与△PEA中,$\left\{\begin{array}{l}{PE=PE}\\{∠EPQ=∠EPA}\\{PA=PQ}\end{array}\right.$,
∴△PEQ≌△PEA,
∴QE=EA,
∴DE=DQ+QE=BD+AE,
∴DE-BD=AE.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,角平分线的判定,正确的作出辅助线构造全等三角形是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
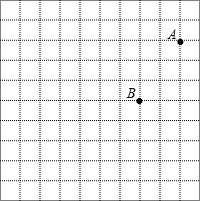 如图是由边长为1的小正方形组成的方格图.
如图是由边长为1的小正方形组成的方格图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,△ABC中,∠BAC为锐角,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE交于H,AD=BD.
如图所示,△ABC中,∠BAC为锐角,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE交于H,AD=BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,D为斜边的中点,点E、点F分别在直线CA、BC上,且DE⊥DF.
如图,在Rt△ABC中,∠ACB=90°,D为斜边的中点,点E、点F分别在直线CA、BC上,且DE⊥DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.
如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
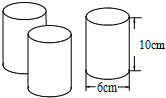 小华家来了两位客人,妈妈冲了900mL的果汁,如果用图中三个大小完全相同的玻璃杯装果汁,这些果汁能将这三个杯子装满吗?请说明理由.(π取3.14)
小华家来了两位客人,妈妈冲了900mL的果汁,如果用图中三个大小完全相同的玻璃杯装果汁,这些果汁能将这三个杯子装满吗?请说明理由.(π取3.14)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com