【题目】为鼓励节约用水，某地推行阶梯式水价计费制，标准如下：每月用水不超过17立方米的按每立方米
元计费，超过17立方米而未超过30立方米的部分按每立方米
元计费，超过30立方米的部分按每立方米
元计费，某户居民上月用水35立方米，应缴水费_________元.
科目：初中数学 来源： 题型：
【题目】超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学尝试用自己所学的知识检测车速．如图，观测点设在A处，离益阳大道的距离(AC)为30米．这时，一辆小轿车由西向东匀速行驶，测得此车从B处行驶到C处所用的时间为8秒，∠BAC＝75°.
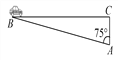
(1)求B、C两点的距离；
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度？
(计算时距离精确到1米，参考数据：sin75°≈0.9659，cos75°≈0.2588，tan75°≈3.732， 
≈1.732，60千米/小时≈16.7米/秒)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若a是不为1的有理数，我们把
称为a的差倒数．如：2的差倒数是
=﹣1，﹣1的差倒数是
．已知a1=﹣
，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，…，依此类推．
（1）分别求出a2，a3，a4的值；
（2）求a1+a2+a3+…+a3600的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列各组式子中：（1）
x2y与﹣xy2；（2）0.5a2b与0.5a2c；（3）3b与3abc；（4）﹣0．1mn2与
mn2中是同类项的有_____（填序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】生活与数学
（1）吉姆同学在某月的日历上利用图1的正方形方框圈出2×2个数，四个数的和是32，那么这四个数是_______________.
（2）玛丽在上面的日历上利用图2的斜框图圈出2×2个数，四个数的和是46，则它们分别是__________.
（3）莉莉也在日历上利用图3的十字框形圈出5个数，它们的和是50，则中间的数是__________.
（4）某月有5个星期日的和是75，则这个月中最后一个星期日是________号.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小虫从
点出发在一条直线上来回爬行，假定向右爬行的路程记作正数，向左爬行的路程记作负数，爬行的各段路程（单位：
）依次为：
.
（1）小虫在爬行过程中离点最远的距离是多少？
（2）小虫爬到最后距点多远？
（3）如果小虫爬行
就奖励它一粒芝麻，那么小虫一共可得到多少粒芝麻？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
分别与
轴、
轴交于
两点，与直线
交于点
.
（1）点
坐标为（ ， ），B为（ ， ）.
（2）在线段
上有一点
，过点作轴的平行线交直线
于点
，设点的横坐标为
，若四边形
是平行四边形时，求出此时的值.
（3）若点
为轴正半轴上一点，且
，则在轴上是否存在一点
，使得
四个点能构成一个梯形若存在，求出所有符合条件的点坐标；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图是由10个同样大小棱长为1的小正方体搭成的几何体，请分别画出它的主视图、左视图和俯视图
（2）这个组合几何体的表面积为 个平方单位（包括底面积）
（3）用小立方体搭一几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，则这样的几何体最多要 个小立方体．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=x+3与两坐标轴交于A，B两点，抛物线y=﹣x2+bx+c过A、B两点，且交x轴的正半轴于点C．
（1）直接写出A、B两点的坐标；
（2）求抛物线的解析式和顶点D的坐标；
（3）在抛物线上是否存在点P，使得△PAB是以AB为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
