
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
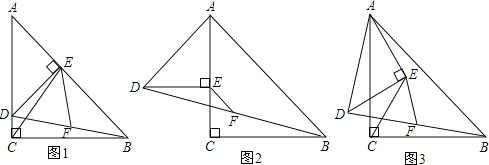
(1)请你探究线段CE与FE之间的数量关系(直接写出结果,不需说明理由);
(2)将图1中的△AED绕点A顺时针旋转,使△AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由;
(3)将图1中的△AED绕点A顺时针旋转任意的角度(如图3),连接BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由.
【答案】(1)线段CE与FE之间的数量关系是CE=![]() FE;(2)(1)中的结论仍然成立.理由见解析;(3)(1)中的结论仍然成立.理由见解析
FE;(2)(1)中的结论仍然成立.理由见解析;(3)(1)中的结论仍然成立.理由见解析
【解析】
(1)连接CF,直角△DEB中,EF是斜边BD上的中线,因此EF=DF=BF,∠FEB=∠FBE,同理可得出CF=DF=BF,∠FCB=∠FBC,因此CF=EF,由于∠DFE=∠FEB+∠FBE=2∠FBE,同理∠DFC=2∠FBC,因此∠EFC=∠EFD+∠DFC=2(∠EBF+∠CBF)=90°,因此△EFC是等腰直角三角形,CF=![]() EF;
EF;
(2)思路同(1)也要通过证明△EFC是等腰直角三角形来求解.连接CF,延长EF交CB于点G,先证△EFC是等腰三角形,可通过证明CF是斜边上的中线来得出此结论,那么就要证明EF=FG,就需要证明△DEF和△FGB全等.这两个三角形中,已知的条件有一组对顶角,DF=FB,只要再得出一组对应角相等即可,我们发现DE∥BC,因此∠EDB=∠CBD,由此构成了两三角形全等的条件.EF=FG,那么也就能得出△CFE是个等腰三角形了,下面证明△CFE是个直角三角形.由上面的全等三角形可得出ED=BG=AD,又由AC=BC,因此CE=CG,∠CEF=45°,在等腰△CFE中,∠CEF=45°,那么这个三角形就是个等腰直角三角形,因此就能得出(1)中的结论了;
(3)思路同(2)通过证明△CFE来得出结论,通过全等三角形来证得CF=FE,取AD的中点M,连接EM,MF,取AB的中点N,连接FN、CN、CF.那么关键就是证明△MEF和△CFN全等,利用三角形的中位线和直角三角形斜边上的中线,我们不难得出EM=PN=![]() AD,EC=MF=
AD,EC=MF=![]() AB,我们只要再证得两对应边的夹角相等即可得出全等的结论.我们知道PN是△ABD的中位线,那么我们不难得出四边形AMPN为平行四边形,那么对角就相等,于是90°+∠CNF=90°+∠MEF,因此∠CNF=∠MEF,那么两三角形就全等了.证明∠CFE是直角的过程与(1)完全相同.那么就能得出△CEF是个等腰直角三角形,于是得出的结论与(1)也相同.
AB,我们只要再证得两对应边的夹角相等即可得出全等的结论.我们知道PN是△ABD的中位线,那么我们不难得出四边形AMPN为平行四边形,那么对角就相等,于是90°+∠CNF=90°+∠MEF,因此∠CNF=∠MEF,那么两三角形就全等了.证明∠CFE是直角的过程与(1)完全相同.那么就能得出△CEF是个等腰直角三角形,于是得出的结论与(1)也相同.
(1)如图1,连接CF,线段CE与FE之间的数量关系是CE=![]() FE;
FE;
解法1:
∵∠AED=∠ACB=90°
∴B、C、D、E四点共圆
且BD是该圆的直径,
∵点F是BD的中点,
∴点F是圆心,
∴EF=CF=FD=FB,
∴∠FCB=∠FBC,∠ECF=∠CEF,
由圆周角定理得:∠DCE=∠DBE,
∴∠FCB+∠DCE=∠FBC+∠DBE=45°
∴∠ECF=45°=∠CEF,
∴△CEF是等腰直角三角形,
∴CE=![]() EF.
EF.
解法2:
易证∠BED=∠ACB=90°,
∵点F是BD的中点,
∴CF=EF=FB=FD,
∵∠DFE=∠ABD+∠BEF,∠ABD=∠BEF,
∴∠DFE=2∠ABD,
同理∠CFD=2∠CBD,
∴∠DFE+∠CFD=2(∠ABD+∠CBD)=90°,
即∠CFE=90°,
∴CE=![]() EF.
EF.
(2)(1)中的结论仍然成立.
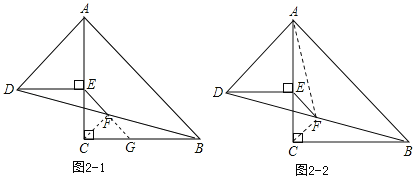
解法1:如图2﹣1,连接CF,延长EF交CB于点G,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠EDF=∠GBF,
又∵∠EFD=∠GFB,DF=BF,
∴△EDF≌△GBF,
∴EF=GF,BG=DE=AE,
∵AC=BC,
∴CE=CG,
∴∠EFC=90°,CF=EF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴CE=![]() FE;
FE;
解法2:如图2﹣2,连结CF、AF,
∵∠BAD=∠BAC+∠DAE=45°+45°=90°,
又点F是BD的中点,
∴FA=FB=FD,
而AC=BC,CF=CF,
∴△ACF≌△BCF,
∴∠ACF=∠BCF=![]() ∠ACB=45°,
∠ACB=45°,
∵FA=FB,CA=CB,
∴CF所在的直线垂直平分线段AB,
同理,EF所在的直线垂直平分线段AD,
又DA⊥BA,
∴EF⊥CF,
∴△CEF为等腰直角三角形,
∴CE=![]() EF.
EF.
(3)(1)中的结论仍然成立.

解法1:如图3﹣1,取AD的中点M,连接EM,MF,取AB的中点N,连接FN、CN、CF,
∵DF=BF,
∴FM∥AB,且FM=![]() AB,
AB,
∵AE=DE,∠AED=90°,
∴AM=EM,∠AME=90°,
∵CA=CB,∠ACB=90°
∴CN=AN=![]() AB,∠ANC=90°,
AB,∠ANC=90°,
∴MF∥AN,FM=AN=CN,
∴四边形MFNA为平行四边形,
∴FN=AM=EM,∠AMF=∠FNA,
∴∠EMF=∠FNC,
∴△EMF≌△FNC,
∴FE=CF,∠EFM=∠FCN,
由MF∥AN,∠ANC=90°,可得∠CPF=90°,
∴∠FCN+∠PFC=90°,
∴∠EFM+∠PFC=90°,
∴∠EFC=90°,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴CE=![]() FE.
FE.


科目:初中数学 来源: 题型:
【题目】如图,过⊙O外一点P作⊙O的两条切线PA,PB,切点分别为A,B.下列结论中:
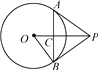
①OP垂直平分AB;
②∠APB=∠BOP;
③△ACP≌△BCP;
④PA=AB;
⑤若∠APB=80°,则∠OBA=40°.
一定正确的是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合),现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图),若有34枚图钉可供选用,则最多可以展示绘画作品( )

A. 16张 B. 18张 C. 20张 D. 21张
查看答案和解析>>
科目:初中数学 来源: 题型:
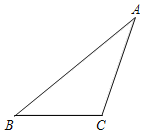
【题目】如图10,在三角形ABC中,∠ACB>90°.
(1)按下列要求画出相应的图形.
①延长BC至点D,使BD=2BC,连接AD;
②过点A画直线BC的垂线,垂足为点E;
③过点C画CG∥AB,CG与AE交于点F,与AD交于点G;
(2)在(1)所画出的图形中,按要求完成下列问题.
①点A、D之间的距离是线段_____的长;点A到线段BC所在的直线的距离是线段___的长,约等于____mm(精确到1mm);
②试说明∠ACD=∠B+∠BAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠1=∠B,∠2=∠3.

(1)试说明AB∥DE;
(2)AF与DC的位置关系如何;为什么;
(3)若∠B=68°,∠C=46°20′,求∠2的度数.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:
(1)∵AD∥BC,(已知)
∴∠1=∠ . ( )
又∵∠1=∠B,(已知)
∴∠B=∠ ,(等量代换)
∴ ∥ . ( )
(2)AF与DC的位置关系是: .理由如下:
∵AB∥DE,(已知)
∴∠2=∠ . ( )
又∵∠2=∠3,(已知)
∴∠ =∠ .(等量代换)
∴ ∥ . ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”“一般”“较强”“很强”四个层次,并绘制成如下两幅尚不完整的统计图.
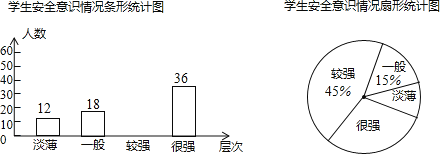
根据以上信息,解答下列问题:
(1)请将条形统计图补充完整;
(2)若“较强”和“很强”均视为安全意识合格,请根据抽样调查的结果,估算该校2000名学生中安全意识合格的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
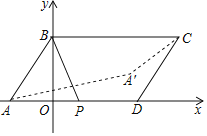
【题目】如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(﹣1,0)、B(0,2)、C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A',则A'C的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
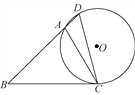
【题目】如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3![]() ,D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
,D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com