
【题目】如图,过⊙O外一点P作⊙O的两条切线PA,PB,切点分别为A,B.下列结论中:
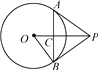
①OP垂直平分AB;
②∠APB=∠BOP;
③△ACP≌△BCP;
④PA=AB;
⑤若∠APB=80°,则∠OBA=40°.
一定正确的是___.
【答案】①③⑤
【解析】由PA、PB是⊙O的两条切线,由切线长定理可得:∠APO=∠BPO,PA=PB,然后由等腰三角形的性质,可得①正确;易证得△ACP≌△BCP;可得③正确,然后由切线的性质,易求得⑤正确.
∵PA、PB是⊙O的两条切线, ∴∠APO=∠BPO,PA=PB,
∴OP垂直平分AB; 故①正确;
∵PB⊥OB,∴∠OBP=90°,∴∠BOP+∠BPO=90°,∴∠BOP+![]() APB=90°,
APB=90°,
得不到∠APB=∠BOP; 故②错误;
在△ACP和△BCP中,PA=PB,PC=PC,AC=BC,∴△ACP≌△BCP;故③正确;
∵PA=PB,但△PAB不一定是等边三角形,∴PA不一定等于AB,故④错误;
∵PA=PB,∴∠PAB=∠PBA,∵∠APB=80°,∴∠ABP=50°,∵∠OBP=90°,
∴∠OBA=40°. ∴正确的是:①③⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
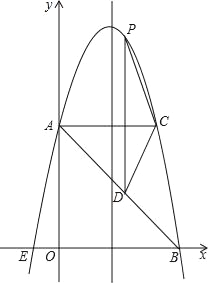
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达
两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达![]() 地后马上以另一速度原路返回
地后马上以另一速度原路返回![]() 地(掉头的时间忽略不计),乙车到达
地(掉头的时间忽略不计),乙车到达![]() 地以后即停在
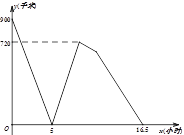
地以后即停在![]() 地等待甲车.如图所示为甲乙两车间的距离
地等待甲车.如图所示为甲乙两车间的距离![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (小时)之间的函数图象,则当乙车到达
(小时)之间的函数图象,则当乙车到达![]() 地的时候,甲车与
地的时候,甲车与![]() 地的距离为__________千米.
地的距离为__________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程![]() 、
、![]() 与时间
与时间![]() 的关系,观察图象并回答下列问题:
的关系,观察图象并回答下列问题:
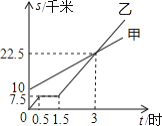
(1)乙出发时,乙与甲相距 千米;
(2)走了一段路程后,乙有事耽搁,停下来时间为 小时;
(3)甲从出发起,经过 小时与乙相遇;
(4)甲行走的平均速度是多少千米![]() 小时?
小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别,某校建立了一个身份识别系绕,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20,如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生,那么表示7班学生的识别图案是( )
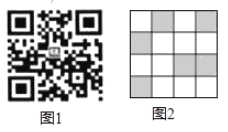
A.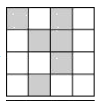 B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
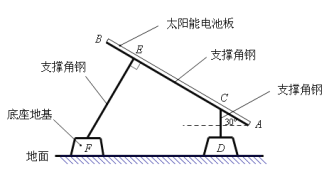
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业,如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为![]() ,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,
,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,![]() 于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)
于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
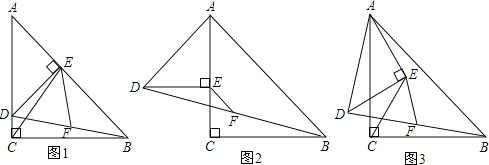
(1)请你探究线段CE与FE之间的数量关系(直接写出结果,不需说明理由);
(2)将图1中的△AED绕点A顺时针旋转,使△AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由;
(3)将图1中的△AED绕点A顺时针旋转任意的角度(如图3),连接BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com