
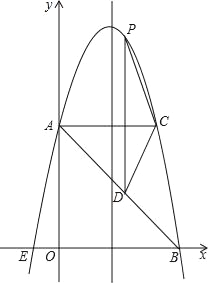
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
【答案】(1)y=﹣x2+4x+5(2)点P(![]() ,
, ![]() )时,S四边形APCD最大=
)时,S四边形APCD最大=![]()
【解析】(1)利用顶点式即可求出二次函数解析式;
(2)先求出直线AB的解析式,设出点P坐标(x,-x2+4x+5),建立函数关系式S四边形APCD=![]() ×AC×PD=2(-x2+5x)=-2x2+10x,根据二次函数求出极值即可.
×AC×PD=2(-x2+5x)=-2x2+10x,根据二次函数求出极值即可.
解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5,
(2)当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=﹣1,n=5,
∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
∵AC=4,
∴S四边形APCD=![]() ×AC×PD=2(﹣x2+5x)=﹣2x2+10x=﹣(x﹣
×AC×PD=2(﹣x2+5x)=﹣2x2+10x=﹣(x﹣![]() )2+
)2+![]() ,
,
∵﹣1<0
∴当x=![]() 时,
时,
∴即:点P(![]() ,
, ![]() )时,S四边形APCD最大=
)时,S四边形APCD最大=![]() .
.


科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发, 到达目的地后停止,设慢车行驶时间为 x 小时,两车之间的距离为 y 千米,两者的关系如图 所示:
(1)两车出发 小时后相遇;
(2)求快车和慢车的速度;
(3)求线段 BC 所表示的 y 与 x 的 关系式,并求两车相距 300 千米时的时间.
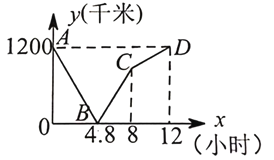
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强市民的节水意识,合理利用水资源,某市采用阶梯收费的调控手段以达到节水的目的,该市自来水收费价目表如下:
每月用水量 | 价格 | 注:水费按月结算,每户每月须缴纳5元污水处理费. |
不超出6m3的部分 | 2元/m3 | |
超出6m3不超出10m3的部分 | 3元/m3 | |
超出10m3的部分 | 5元/m3 |
若某户居民![]() 月份用水
月份用水![]() ,则应缴费
,则应缴费![]() (元),
(元),
(1)若用户![]() 月份共用水
月份共用水![]() ,则需缴费________;
,则需缴费________;
(2)若该户居民某月缴费![]() 元,则该户居民该月用水多少吨?
元,则该户居民该月用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=3x2+36x+81.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标;
(4)当x取何值时,y有最小值,并求出最小值;
(5)当x取何值时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
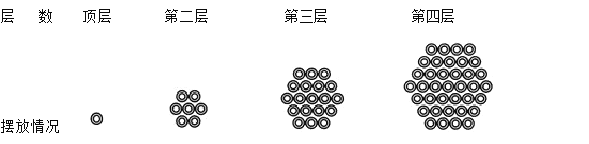
【题目】如图所示,某公园设计节日鲜花摆放方案,其中一个花坛由一批花盆堆成六角垛,顶层一个,以下各层堆成六边形,逐层每边增加一个花盆,若这垛花盆底层最长的一排共13个花盆,则底层的花盆的个数是( )
A.91B.127C.169D.255
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB∥CD,点 E 为射线 FG 上一点.
(1)如图 1,若∠EAF=30°,∠EDG=40°,则∠AED= °;
(2)如图 2,当点 E 在 FG 延长线上时,此时 CD 与 AE 交于点 H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图 3,DI 平分∠EDC,交 AE 于点 K,交 AI 于点 I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为
都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为![]() ,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于
,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于![]() 之间部分的长度和为y,则y关于x的函数图象大致为( )
之间部分的长度和为y,则y关于x的函数图象大致为( )

A. 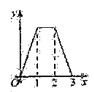 B.
B. 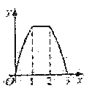 C.
C. 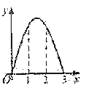 D.
D. 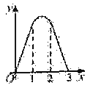
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为准备联合韵律操表演,甲、乙两校共100人准备统一购买服装(一人买一套)参加表演,其中甲校人数多于乙校人数,下面是服装厂给出的演出服装的价格表:

如果两所学校分别单独购买服装,一共应付5710元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加表演?
(3)如果甲校有9名同学抽调去参加迎奥运书法比赛不能参加演出,那么你有几种购买方案,通过比较,你该如何购买服装才能最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过⊙O外一点P作⊙O的两条切线PA,PB,切点分别为A,B.下列结论中:
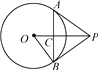
①OP垂直平分AB;
②∠APB=∠BOP;
③△ACP≌△BCP;
④PA=AB;
⑤若∠APB=80°,则∠OBA=40°.
一定正确的是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com