
【题目】已知,AB∥CD,点 E 为射线 FG 上一点.
(1)如图 1,若∠EAF=30°,∠EDG=40°,则∠AED= °;
(2)如图 2,当点 E 在 FG 延长线上时,此时 CD 与 AE 交于点 H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图 3,DI 平分∠EDC,交 AE 于点 K,交 AI 于点 I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD 的度数.

【答案】(1)70;(2)∠EAF=∠AED+∠EDG,理由见解析;(3) 142°
【解析】(1)延长 DE 交 AB 于 H,由两直线平行内错角相等,得到∠D=∠AHE=40° ,再由三角形外角的性质即可求得∠AED度数;
(2)根据∠EHG是△DEH的外角,即可得出∠EHG=∠AED+∠EDG,进而得到∠EAF=∠AED+∠EDG;
(3)设∠EAI=α,则∠BAE=3α,由三角形内角和定理得∠EDK=α﹣2°,由角平分线定义,得∠CDE =2α﹣4°,再由两直线平行,同位角相等得3α=22°+2α-4°,从而解得∠EDK=16°,在△DKE 中,由三角形内角和定理可求得∠EKD=142°.
(1)如图,延长DE交AB于H,
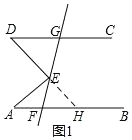
∵AB∥CD,
∴∠D=∠AHE=40°,
∵∠AED是△AEH的外角,
∴∠AED=∠A+∠AHE=30°+40°=70°,
故答案为:70;
(2)∠EAF=∠AED+∠EDG.
理由:∵AB∥CD,
∴∠EAF=∠EHC,
∵∠EHC 是△DEH 的外角,
∴∠EHG=∠AED+∠EDG,
∴∠EAF=∠AED+∠EDG;
(3)∵∠EAI:∠BAI=1:2,
∴设∠EAI=α,则∠BAE=3α,
∵∠AED=22°,∠I=20°,∠DKE=∠AKI,
又∵∠EDK+∠DKE+∠DEK=180°,∠KAI+∠KIA+∠AKI=180°,
∴∠EDK=α﹣2°,
∵DI 平分∠EDC,
∴∠CDE=2∠EDK=2α﹣4°,
∵AB∥CD,
∴∠EHC=∠EAF=∠AED+∠EDG,
即3α=22°+2α-4°, 解得α=18°,
∴∠EDK=16°,
∴在△DKE 中,∠EKD=180°﹣16°﹣22°=142°.


科目:初中数学 来源: 题型:
【题目】△ABC 中,已知点 D,E,F 分别是 BC,AD,CE 边上的中点,且 S△ABC=4cm2 则 S△BEF 的值为( )
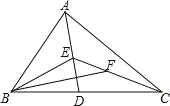
A. 2cm2 B. 1cm2 C. 0.5cm2 D. 0.25cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
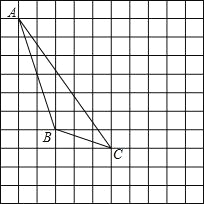
【题目】如图,每个小正方形的边长为 1 个单位,每个小方格的顶点叫格点.
(1)画出△ABC 的 AB 边上的中线 CD;
(2)画出△ABC 向右平移 4 个单位后得到的△A1B1C1;
(3)图中 AC 与 A1C1 的关系是: ;
(4)图中△ABC 的面积是 ;
(5)能使△BCE 面积为 3 的格点 E 有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示:
(1)A、B两城之间距离是多少千米?
(2)求乙车出发多长时间追上甲车?
(3)直接写出甲车出发多长时间,两车相距20千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
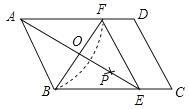
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是 ;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 ,∠ABC= °.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的有( )
①相等的角是对顶角.
②在同一平面内,若a∥b,b∥c,则a∥c.
③若点P(m+3,m+1)在x轴上,则点P的坐标为(4,0).
④数轴上每一个点都表示唯一一个实数.
⑤若a大于0,b不大于0,则点P(-a,-b)在第三象限.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com