练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知如图所示， 与 关于点 成中心对称，连接 ， ．

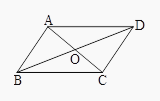
    （1）求证：四边形 是平行四边形；
    （2）若 的面积为15 ，求四边形 的面积．

    【答案】
    （1）

    证明：∵ 与 关于点 成中心对称，∴ 即四边形 的对角线互相平分，∴四边形 是平行四边形.


    （2）

    解：记 底边上的高为h，那么平行四边形ABCD底边AB上的为2h，因为 的面积为15，所以 ，所以2ABh＝60，所以平行四边形ABCD的面积为60 ．


    【解析】（2）的关键在于明白： 底边上的高为平行四边形ABCD底边AB上的为一半．
    【考点精析】根据题目的已知条件，利用平行四边形的判定和中心对称及中心对称图形的相关知识可以得到问题的答案，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形；如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读理解题：

    定义：如果一个数的平方等于﹣1，记为i2=﹣1，这个数i叫做虚数单位．那么和我们所学的实数对应起来就叫做复数，表示为a+bi（a，b为实数），a叫这个复数的实部，b叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似．

    例如计算：（2+i）+（3﹣4i）=5﹣3i．

    （1）填空：i4=　 　，i5=　 　．

    （2）计算：①（4+i）（4﹣i）； ②（3+i）2；

    （3）若两个复数相等，则它们的实部和虚部必须分别相等，完成下列问题：已知：（x+y）+3i=（1﹣x）﹣yi，（x，y为实数），求x，y的值．

    （4）试一试：请利用以前学习的有关知识将化简成a+bi的形式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将二次函数y=31x2-999x+892的图形画在坐标平面上，判断方程31x2-999x+892=0的两根，下列叙述何者正确（　　）

    A.两根相异，且均为正根
    B.两根相异，且只有一个正根
    C.两根相同，且为正根
    D.两根相同，且为负根

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一点A从数轴上表示+2的点开始移动，第一次先向左移动1个单位，再向右移动2个单位；第二次先向左移动3个单位，再向右移动4个单位；第三次先向左移动5个单位，再向右移动6个单位……

    （1）写出第一次移动后这个点在数轴上表示的数为 ；

    （2）写出第二次移动后这个点在数轴上表示的数为 ；

    （3）写出第五次移动后这个点在数轴上表示的数为 ；

    （4）写出第次移动结果这个点在数轴上表示的数为 ；

    （5）如果第次移动后这个点在数轴上表示的数为56，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中真命题是（ ）
    A.两个等腰三角形一定全等
    B.正多边形的每一个内角的度数随边数增多而减少
    C.菱形既是中心对称图形，又是轴对称图形
    D.两直线平行，同旁内角相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列算式
    ① =±3；② =9；③26÷23=4；④ =2016；⑤a+a=a2 ．
    运算结果正确的概率是（　　）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正比例函数y＝kx的图象经过点P(1，2)，如图所示．

    (1)求这个正比例函数的解析式；

    (2)将这个正比例函数的图象向右平移4个单位长度，求出平移后的直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我县各中小学校积极组织学生开展课外阅读活动，为了解某校学生每周课外阅读的时间量t(单位：小时)，采用随机抽样的方法抽取部分学生进行了问卷调查，调查结果按0≤t〈2,2≤t〈3,3≤t〈4，t≥4分为四个等级，并分别用A、B、C、D表示.根据调查结果统计数据绘制成如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：

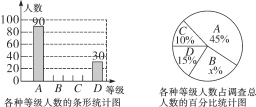
    (1)求这次抽查的学生总数是多少人，并求出x的值；

    (2)将不完整的条形统计图补充完整；

    (3)若该校共有学生3600人，试估计每周课外阅读时间量满足2≤t〈4的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，AB∥CD，点 E 为射线 FG 上一点．

    (1)如图 1，若∠EAF=30°，∠EDG=40°，则∠AED= °；

    (2)如图 2，当点 E 在 FG 延长线上时，此时 CD 与 AE 交于点 H，则∠AED、∠EAF、∠EDG之间满足怎样的关系，请说明你的结论；

    (3)如图 3，DI 平分∠EDC，交 AE 于点 K，交 AI 于点 I，且∠EAI：∠BAI=1：2，∠AED=22°，∠I=20°，求∠EKD 的度数．

    查看答案和解析>>

    同步练习册答案